5장 정형 데이터 마이닝
1절 데이터 마이닝의 개요
1. 데이터 마이닝
가. 개요
· 데이터마이닝은 대용량 데이터에서 의미있는 패턴을 파악하거나 예측하여 의사결정에 활용하는 방법
나. 통계분석과의 차이점
· 통계분석은 가설이나 가정에 따른 분석이나 검증을 하지만 데이터마이닝은 다양한 수리 알고리즘을 이용해 데이터베이스의 데이터로부터 의미있는 정보를 찾아내는 방법을 통칭
다. 종료
| 정보를 찾는 방법론에 따른 종류 | 분석대상, 활용목적, 표현방법에 따른 분류 | ||||||||||||
| · 최근접이웃(Nearest Neighborhood) | · 포케스팅(Forecasting) | ||||||||||||
라. 사용분야(매우 다양)
마. 데이터마이닝의 최근환경
· 데이터마이닝 도구가 다양하고 체계화되어 환경에 적합한 제품을 선택하여 활용 가능
· 통계학 전문가와 대기업 위주 시장, 쓰기 힘들고 단순 반복작업이 많아 실무에서 적극 이용되기 어려움, 데이터 준비를 위한 추출 · 가공부담, 경영진과 어려운 소통, 데이터 핸들링에만 사용, 신뢰부족
· 분석 결과의 품질은 분석가의 경험과 역량에 따라 차이
· 분석과제의 복잡성이나 중요도가 높으면 풍부함 경험을 가진 전문가에 의뢰할 필요
2. 데이터마이닝의 분석방법
| Supervised Data Prediction(지도학습) | Unsupervised Data Prediction(비지도 학습) |
· 최근접 이웃법(KNN, K-Nearest Neighbor) |
· SOM(Self Organizing Map) |
3. 분석목적에 따른 작업 유형과 기법
| 목적 | 작업유형 | 설명 | 사용기법 | ||
Modeling |
Classification |
가장 많이 사용되는 직업으로 과거의 데이터로부터 고객 특성을 찾아내어 분류모형을 만들어 이를 토대로 새로운 레코드의 결과값을 예측하는 것을 목표로 마케팅 및 고객 신용평가 모형에 활용됨 | 회귀분석, 판별분석, 신경망,의사결정나무 | ||
Modeling |
Association |
데이터 안에 존재한느 항목간의 종속관계를 찾아내는 작업으로, 제품이나 서비스 교차판매(Cross Selling), 매장진열(Display), 첨부우편(Attached Mailings), 사기적발(Fraud Detection) 등의 다양한 분야에 활용됨 | 동시발생 매트릭스 | ||
Sequence |
연관 규칙에 시간관련 정보가 포함된 형태로, 고객의 구매이력(History) 속성이 반드시 필요하며, 목표 마케팅(Target Marketing)이나 일대일 마케팅(One to One Marketing)에 활용됨 | 동시발생 매트릭스 | |||
Clustering |
고객 레코드들을 유사한 특성을 지닌 몇 개의 소그룹으로 분할하는 작업으로 작업의 특성이 분류규칙(Classification)과 유사하나 분석대상 데이터에 결과 값이 없으며, 판촉활동이나 이벤트 대상을 선정하는데 활용됨. | K-Means Clustering |
4. 데이터 마이닝 추진단계
· 데이터 마이닝은 일반적으로 목적 정의, 데이터 준비, 데이터 가공, 데이터 마이닝 기법적용, 검증단계로 추진
가. 1단계 : 목적 설정(목적정의 단계부터 시작)
· 데이터마이닝을 통해 무엇을 왜 하는지 명확한 목적(이해관계자 모두 동의하고 이해할 수 있는)을 설정
· 전문가가 참여해 목적에 따라 사용할 모델과 필요한 데이터를 정의
나. 2단계 : 데이터 준비
· 고객정보, 거래정보, 상품 마스터정보, 웹로그 데이터, 소셜 네트워크 데이터 등 다양한 데이터를 활용
· IT부서와 사전에 협의하고 일정을 조율하여 데이터 접근 부하에 유의, 필요시 다른 서버에 저장하여 운영
· 데이터 정제를 통해 데이터의 품질을 보장하고, 필요시 데이터를 보강하여 충분한 양의 데이터를 확보
다. 3단계 : 가공
· 모델 개발 단계에서 데이터 읽기, 데이터 마이닝에 부하걸림 → 모델링 일정계획을 팀원간 잘 조정
· 모델링 목적에 따라 목적변수를 정의
· 필요한 데이터를 데이터마이닝 소프트웨어에 적용할 수 있는 형식으로 가공
라. 4단계 : 기법적용
· 1단계에서 명확한 목적에 맞게 데이터마이닝 기법을 적용하여 정보를 추출
· 적용할 데이터 마이닝 기법은 1단계에서 이미 결정 됬어야 바람직
· 데이터 마이닝 모델을 목적에 맞게 선택하고 SW사용하는데 필요한 값 지정
· 어떤 기법을 활용하고 어떤값을 입력하느냐 등은 데이터 분석가의 전문성에 따라 다름.
· 데이터 마이닝의 적용목적, 보유데이터, 산출되는 정보등에 따라 적절한 SW 기법선정
마. 5단계 : 검증
· 데이터마이닝으로 추출된 정보를 검증
· 테스트 데이터와 과거 데이터를 활용
· 검증이 완료되면 IT부서와 협의해 상시 데이터 마이닝 결과를 업무에 적용하고 보고서를 작성하여 추가수익과 투자대비성과(ROI)등으로 기대효과를 전파
5. 데이터마이닝을 위한 데이터 분할
가. 개요
· 결과 신빙성 검증을 위해 일반적으로 구축용, 검정용, 시험용으로 분리
나. 데이터 분할
1) 구축용(training data, 50%)
· 추정용 훈련용 데이터라고도 불리며 데이터마이닝 모델을 만드는데 활용
2) 검정용(validation data, 30%)
· 구축된 모형의 과대 추정 또는 과소추정을 미세 조정을 하는데 활용
3) 시험용(test data, 20%)
· 테스트 데이터나 과거 데이터를 활용하여 모델의 성능을 검증하는데 활용
· 데이터마이닝 추진 5단계(검증)에서 검증용으로 사용
4) 데이터양이 충분하지 않거나 입력변수에 대한 설명이 충분한 경우
· 구축용과 시험용으로만 분해하여 사용하기도 함
① 홀드아웃(hold-out)
· 원본데이터를 랜덤하게 두 분류(training set/test set)로 분리하여 교차검증하는 방법
· 모형의 학습 및 구축을 위한 훈련용 자료로 하나는 성과 평가를 위한 검증자료로 사용
· 전체 데이터 중 70%를 훈련용으로 나머지는 검증용으로 사용
· 검증용 자료의 결과는 성과 측정만을 위해 사용
② 교차검증(cross-validation)
· 주어진 데이터를 가지고 반복적으로 성과를 측정하여 그 결과를 평균한 것으로 분석모형을 평가하는 방법
· 대표적인 교차검증 k-fold

③ 붓스트랩
· 평가를 반복하는 측면에서 교차검증과 유사하나 훈련용 자료를 반복 재선정 한다는 점에서 차이가 있음
· 관측치를 한번이상 훈련용 자료로 복원추출법에 기반함
· 복원추출법

· 전체 데이터의 양이 크지 않은 경우의 모형 평가에 가장 적합
· 일반적인 예제로 0.632 붓스트랩을 들 수 있음(63.2% : training set, 36.8% : test set)

※ 데이터 마이닝 모닝 평가
· 데이터 마이닝 프로젝트의 목적과 내용에 따라 적합모형 다름
- 몇가지 모형 대안 놓고 어느 것이 적합한지 가장 보편적 기준 : 손익 비교
· 모델링의 변경 주기가 있으며 근본적으로 정확도의 편차가 급증하는 시점에 실행
- classification : 최소 1년 2번
- 연관성규칙 : 비즈니스 특성에 따라 1주/1개월
- forecasting : 일 · 주 · 월단위등모델링의기준에따라다름
· 성공적인 데이터 마이닝 핵심 : 전반적인 비즈니스 프로세스에 대한 이해
- 각 프로세스에서 어떤 형태로 데이터가 발생되 변형 · 축적 되는지 이해하고 필요한 데이터 선별가능 해야함
- 데이터에 대한 전반적인 파악, 팩트와 특이사항 파악해 브레인 스트림, 마트 잘만들기(자동화), 모델링(처음부터 데이터 접근X, 샘플링 최대한 활용)
6. 성과분석
가. 오류분포에 대한 추정치
· TP : 실제값과 예측값이 모두 True인 빈도
· TN : 실제값과 예측값이 모두 False인 빈도
· FP : 실제값은 False이나 True로 예측한 빈도
· FN : 실제값은 True이나 False로 예측한 빈도

· 암여부 판단(100% 모델)





· F1 Score

나. ROCR 패키지로 성과분석
1) ROC Curve(Receiver Operating Characteristics Curve)
· ROC Curve란 가로축을 FPR(False Positive Rate=1-특이도)값으로 두고, 세로축을 TPR(True Positive Rate, 민감도) 값으로 두어 시각화한 그래프
· 2진분류(binary classification)에서 모형의 성능을 평가하기 위해 많이 사용되는 척도
· 그래프가 왼쪽 상단에 가깝게 그려질수록 올바르게 예측한 비율은 높고, 잘못 예측한 비율은 낮음
· ROC 곡선 아래 면적을 의미하는 AUROC(Area Under ROC)값이 크면 클수록(1에 가까울수록) 모형의 성능이 좋다고 평가
· AUROC(Area Under ROC)를 이용한 정확도의 판단기준
| 기준 | 구분 |
| 0.9 - 1.0 | excellent(A) |
| 0.8 - 0.9 | good |
| 0.7 - 0.8 | fair |
| 0.6 - 0.7 | poor |
| 0.5 - 0.6 | fail |
다. 이익도표(Lift chart)
※ 이익도표와 향상도 곡선
· 이익 : 목표범주에 속하는 개체들이 각 등급에 얼마나 분포하고 있는지 나타내는 값
· 이익도표 : 해당 등급에 따라 계산된 이익값을 누적으로 연결한 도표
→ 분류된 관측치가 각 등급별 얼마나 포함되는지 나타내는 도표
· 향상도 곡선
- 랜덤모델과 비교하여 해당 모델의 성과가 얼마나 향상되었는지 등급별로 파악하는 그래프
- 상위 등급은 향상도가 매우 크고 하위로 갈수록 향상도가 감소되어 예측력이 적절함을 의미
- 등급에 관계없이 향상도에 차이가 없으면 예측력이 좋지 않음


2절 분류분석
1. 분류분석과 예측분석
가. 분류분석의 정의
· 데이터가 어떤 그룹에 속하는지 예측하는데 사용되는 기법
- 분류모델을 개발할 때는 train data / test data 구분지어 모델링
· 전체 데이터를 7:3, 8:2 등으로 나눠 train해서 최적모델 확정짓고 test를 검증
· train과 test간 편차 없어야 하며 성능은 test가 다소 낮게 나오는 경향
· 특정 등급으로 나누는 점에서 군집분석과 유사하나 각 계급이 어떻게 정의되는지 미리 알아야 함.
- 분류(classification) : 객체를 정해 놓은 범주로 분류하는데 목적. CRM에서는 고객 행동 예측, 속성 파악에 응용. 다양한 분야에서 활용가능
※ 모형평가
· 분류분석의 모형의 평가는 예측 및 분류를 위해 구축된 모형이 임의의 모형보다 우수한 분류 성과를 보이는 지와 고려된 서로 다른 모형들 중 어느것이 우수한 예측분류 성과를 가장 적합한 모형을 선택하기 위해서는 성과 평가의 기준이 필요
· 모형평가의 기준
- 일반화의 가능성 → 다른 모집단 내에 적용시에도 동일한 결과 기준
- 효율성 → 적은 입력 변수
- 예측과 분류의 정확성 → 실제로 적용시
바. 분류기법(분류를 위해 데이터 마이닝 기법)
· 회귀분석, 로지스틱 회귀분석(Logistic Regression)
· 의사결정나무(Decision Tree), CART(Classification and Regression Tree), C5.0
· 베이지안 분류(Bayesian Classification), Naive Bayesion
· 인공신경망(ANN, Artificial Neutral Network)
· 지지도벡터기계(SVM, Support Vector Machine)
· 상황판단, 속하는 분류집단 특성, 예측등에도 사용
2. 로지스틱(이항분포) 회귀분석(Logistic Regression)
· 분석하고자 하는 대상들이 두 집단 혹은 그 이상의 집단(다변수 데이터)으로 나누어진 경우에 개별 관측치들이 어느 집단으로 분류될 수 있는가를 분석하고 이를 예측하는 모형을 개발하는데 사용되는 대표적인 통계 알고리즘
· 분석목적이나 절차에 있어서는 일반회귀분석과 유사하나 종속변수가 명목척도로 측정된 범주형 질적변수인 경우에 사용한다는 점에서 일반회귀분석과 차이가 있다.


> #로지스틱 회귀분석
> require(survival)
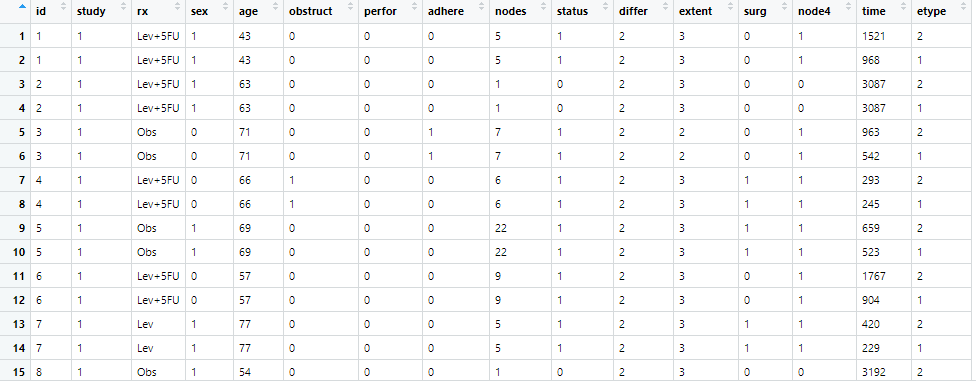
> str(colon)
'data.frame': 1858 obs. of 16 variables:
$ id : num 1 1 2 2 3 3 4 4 5 5 ...
$ study : num 1 1 1 1 1 1 1 1 1 1 ...
$ rx : Factor w/ 3 levels "Obs","Lev","Lev+5FU": 3 3 3 3 1 1 3 3 1 1 ...
$ sex : num 1 1 1 1 0 0 0 0 1 1 ...
$ age : num 43 43 63 63 71 71 66 66 69 69 ...
$ obstruct: num 0 0 0 0 0 0 1 1 0 0 ...
$ perfor : num 0 0 0 0 0 0 0 0 0 0 ...
$ adhere : num 0 0 0 0 1 1 0 0 0 0 ...
$ nodes : num 5 5 1 1 7 7 6 6 22 22 ...
$ status : num 1 1 0 0 1 1 1 1 1 1 ...
$ differ : num 2 2 2 2 2 2 2 2 2 2 ...
$ extent : num 3 3 3 3 2 2 3 3 3 3 ...
$ surg : num 0 0 0 0 0 0 1 1 1 1 ...
$ node4 : num 1 1 0 0 1 1 1 1 1 1 ...
$ time : num 1521 968 3087 3087 963 ...
$ etype : num 2 1 2 1 2 1 2 1 2 1 ...
> colon1<-na.omit(colon)
> View(colon)
> result<-glm(status~rx+sex+age+perfor+adhere+nodes+differ+extent+surg,family = binomial,data=colon1)
> result
Call: glm(formula = status ~ rx + sex + age + perfor + adhere + nodes +
differ + extent + surg, family = binomial, data = colon1)
Coefficients:
(Intercept) rxLev rxLev+5FU sex age perfor adhere nodes differ
-2.365671 -0.068786 -0.589793 -0.093036 0.001124 0.126985 0.376389 0.183540 0.031927
extent surg
0.574665 0.391165
Degrees of Freedom: 1775 Total (i.e. Null); 1765 Residual
Null Deviance: 2462
Residual Deviance: 2243 AIC: 2265
> summary(result)
Call:
glm(formula = status ~ rx + sex + age + perfor + adhere + nodes +
differ + extent + surg, family = binomial, data = colon1)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.5811 -1.0480 -0.5899 1.1300 2.0642
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.365671 0.475809 -4.972 6.63e-07 ***
rxLev -0.068786 0.122349 -0.562 0.57397
rxLev+5FU -0.589793 0.124437 -4.740 2.14e-06 ***
sex -0.093036 0.101457 -0.917 0.35914
age 0.001124 0.004293 0.262 0.79347
perfor 0.126985 0.298253 0.426 0.67028
adhere 0.376389 0.147220 2.557 0.01057 *
nodes 0.183540 0.018831 9.747 < 2e-16 ***
differ 0.031927 0.100696 0.317 0.75120
extent 0.574665 0.116465 4.934 8.05e-07 ***
surg 0.391165 0.113692 3.441 0.00058 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2461.7 on 1775 degrees of freedom
Residual deviance: 2243.4 on 1765 degrees of freedom
AIC: 2265.4
Number of Fisher Scoring iterations: 4
> reduced.model=step(result)
Start: AIC=2265.38
status ~ rx + sex + age + perfor + adhere + nodes + differ +
extent + surg
Df Deviance AIC
- age 1 2243.4 2263.4
- differ 1 2243.5 2263.5
- perfor 1 2243.6 2263.6
- sex 1 2244.2 2264.2
<none> 2243.4 2265.4
- adhere 1 2250.0 2270.0
- surg 1 2255.3 2275.3
- rx 2 2270.1 2288.1
- extent 1 2269.7 2289.7
- nodes 1 2364.7 2384.7
Step: AIC=2263.45
status ~ rx + sex + perfor + adhere + nodes + differ + extent +
surg
Df Deviance AIC
- differ 1 2243.6 2261.6
- perfor 1 2243.6 2261.6
- sex 1 2244.3 2262.3
<none> 2243.4 2263.4
- adhere 1 2250.1 2268.1
- surg 1 2255.4 2273.4
- rx 2 2270.2 2286.2
- extent 1 2269.8 2287.8
- nodes 1 2365.5 2383.5
Step: AIC=2261.55
status ~ rx + sex + perfor + adhere + nodes + extent + surg
Df Deviance AIC
- perfor 1 2243.7 2259.7
- sex 1 2244.4 2260.4
<none> 2243.6 2261.6
- adhere 1 2250.4 2266.4
- surg 1 2255.5 2271.5
- rx 2 2270.2 2284.2
- extent 1 2270.2 2286.2
- nodes 1 2369.6 2385.6
Step: AIC=2259.72
status ~ rx + sex + adhere + nodes + extent + surg
Df Deviance AIC
- sex 1 2244.5 2258.5
<none> 2243.7 2259.7
- adhere 1 2251.0 2265.0
- surg 1 2255.8 2269.8
- rx 2 2270.3 2282.3
- extent 1 2270.6 2284.6
- nodes 1 2370.0 2384.0
Step: AIC=2258.53
status ~ rx + adhere + nodes + extent + surg
Df Deviance AIC
<none> 2244.5 2258.5
- adhere 1 2252.0 2264.0
- surg 1 2256.6 2268.6
- rx 2 2270.6 2280.6
- extent 1 2271.3 2283.3
- nodes 1 2371.3 2383.3
> summary(reduced.model)
Call:
glm(formula = status ~ rx + adhere + nodes + extent + surg, family = binomial,
data = colon1)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.570 -1.068 -0.593 1.122 2.031
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.29072 0.35054 -6.535 6.37e-11 ***
rxLev -0.07207 0.12207 -0.590 0.554906
rxLev+5FU -0.58212 0.12413 -4.690 2.74e-06 ***
adhere 0.39433 0.14498 2.720 0.006530 **
nodes 0.18435 0.01849 9.971 < 2e-16 ***
extent 0.57690 0.11607 4.970 6.68e-07 ***
surg 0.39294 0.11355 3.460 0.000539 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2461.7 on 1775 degrees of freedom
Residual deviance: 2244.5 on 1769 degrees of freedom
AIC: 2258.5
Number of Fisher Scoring iterations: 4
* view(colon)
3. 의사결정나무
· 나무의 구조에 가반한 예측 모델을 갖는 데이터를 분류하기 위한 질문, 잎은 분류 결과에 따라 분리된 데이터 의미
가. 정의
· 분류함수를 의사결정 규칙으로 이뤄진 나무 모양으로 그리는 방법
· 연속적으로 발생하는 의사결정 문제를 시각화해 의사결정이 이뤄지는 시점과 성과를 한눈에 볼 수 있게 함
· 해석이 간편
· 깊이(depth) : 뿌리마디부터 끝마디까지의 중간마디들의 수 |
> # party 패키지(unbiased recursive based on permutatio test 방법을 이용)
> # 입력변수의 레벨이 31개로 제한
> # 과대적합
> # training set이 정확한 결과를 보여주기 위해서 복잡하게 모델을 만드는 것(Over fitting)
> # 과소적합
> # 모델이 너무 간단해서 정확도가 낮은 모델(Under fitting)
> # 과대 적합은 training data에서는 정확도가 높지만, 새로운 데이터가 입력되면 잘못 예측할 수 있다.
> # 과소 적합은 training data조차도 정확도가 떨어진다.
> ## 과대적합과 과소적합의 문제점을 해결하기 위해서는 더만혹 더다양한 데이터를 확보하고,
> ## 확보한 데이터로 부터 다양한 특징을 찾아내는 것
> library(rpart)
> m<-rpart(Species~.,data=iris)
> m
n= 150
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 150 100 setosa (0.33333333 0.33333333 0.33333333)
2) Petal.Length< 2.45 50 0 setosa (1.00000000 0.00000000 0.00000000) *
3) Petal.Length>=2.45 100 50 versicolor (0.00000000 0.50000000 0.50000000)
6) Petal.Width< 1.75 54 5 versicolor (0.00000000 0.90740741 0.09259259) *
7) Petal.Width>=1.75 46 1 virginica (0.00000000 0.02173913 0.97826087) *
> # n= 150 150개 데이터
> # 1) root 150 100 setosa (0.33333333 0.33333333 0.33333333) 뿌리노드 150개데이터 100 손실율
> # (0.33333333 0.33333333 0.33333333) 전체 품종의 비율
> plot(m,compress = T,margin =.3)
경고메시지(들):
1: In Ops.factor(left, right) : ‘&’ not meaningful for factors
2: In if (compress & missing(nspace)) nspace <- branch :
length > 1 이라는 조건이 있고, 첫번째 요소만이 사용될 것입니다
3: In Ops.factor(left) : ‘!’ not meaningful for factors
4: In if (!compress) nspace <- -1L :
length > 1 이라는 조건이 있고, 첫번째 요소만이 사용될 것입니다
> text(m,cex=1.5)#글자크기 증가
> # 6) Petal.Width< 1.75 54 5 versicolor (0.00000000 0.90740741 0.09259259) *
> # 54개중에 49개가 versicolor
> #7) Petal.Width>=1.75 46 1 virginica (0.00000000 0.02173913 0.97826087) *
> # 46개중에 45개는 virginica* plot(m,compress = T, margin = .3)

* plot(m,compress = T, margin = .3)

#install.packages("rpart.plot")
library(rpart.plot)
prp(m,type=4,extra=2,digits=3

> rpart.pred<-predict(m, newdata=iris,type="class")
> #install.packages("caret")
> #install.packages("e1071")
> library(caret)
> #Accuracy : 0.96 정확도 96
> confusionMatrix(rpart.pred, iris$Species)
Confusion Matrix and Statistics
Reference
Prediction setosa versicolor virginica
setosa 50 0 0
versicolor 0 49 5
virginica 0 1 45
Overall Statistics
Accuracy : 0.96
95% CI : (0.915, 0.9852)
No Information Rate : 0.3333
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.94
Mcnemar's Test P-Value : NA
Statistics by Class:
Class: setosa Class: versicolor Class: virginica
Sensitivity 1.0000 0.9800 0.9000
Specificity 1.0000 0.9500 0.9900
Pos Pred Value 1.0000 0.9074 0.9783
Neg Pred Value 1.0000 0.9896 0.9519
Prevalence 0.3333 0.3333 0.3333
Detection Rate 0.3333 0.3267 0.3000
Detection Prevalence 0.3333 0.3600 0.3067
Balanced Accuracy 1.0000 0.9650 0.9450바. 나무의 성장
3) 정지 규칙(stopping rule)
· 더 이상 분리가 일어나지 않고, 현재의 마디가 끝마디가 되도록 하는 규칙
· 정지기준(stoppig criterion) : 의사결정나무의 깊이(depth)를 지정, 끝마디의 레코드 수의 최소 개수를 지정
4. 불순도의 열러가지 측도
· 목표변수가 범주형 변수인 의사결정나무의 분류규칙을 선택하기 위해서는 카이제곱 통계량, 지니지수, 엔트로피 지수를 활용한다.
1) 카이제곱 통계량
· 카이제곱 통계량은 각 셀에 대한 ((실제도수-기대도수)의 제곱/기대도수)의 합으로 구할 수 있음
· 기대도수 = 열의 합계 X 합의 합계 / 전체 합계

2) 지니지수
· 노드의 불순도를 나타내는 값
· 지니지수의 값이 클수록 이질적(Diversity)이며 순수도(Purity)가 낮다고 볼 수 있음
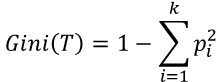
3) 엔트로피 지수
· 열학학에서 쓰는 개념으로 무질서 정도에 대한 측도
· 엔트로피 지수의 값이 클수록 순수도(Purity)가 낮다고 볼 수 있음
· 엔트로피 지수가 가장 작은 예측 변수와 이때의 최적분리 규칙에 의해 자식마디를 형성

5. 의사결정나무 알고리즘
가. CART(Classification and Regression Tree)
· 불순도의 측도로 출력(목적) 변수가 범주형일 경우 지니지수를 이용, 연속형인 경우 분산을 이용한 이진분리(binary split)를 사용한다.
· 개별 입력변수 뿐만 아니라 입력변수들의 선형결합들 중에서 최적의 분리를 찾을 수 있음
나. C4.5와 C5.0
· CART와는 다르게 각 마디에서 다지분리(multiple split)가 가능하며 범주형 입력변수에 대해서는 범주의 수만큼 분리가 일어남
· 불순도의 측도로는 엔트로피지수를 사용
다. CHAID(CHi-squared Automatic Interaction Detection)
· 가지치기를 하지 않고 적당한 크기에서 나무모형의 성장을 중지하며 입력변수가 반드시 범주형 변수여야 함
· 불순도의 측도로는 카이제곱 통계량을 사용
3절 앙상블 분석
가. 정의
· 주어진 자료로부터 여러 개의 예측모형들을 만든 후 예층모형들을 조합하여 하나의 최종 예측모형을 만드는 방법으로 다중 모델 조합(combining multiple models), 분류기 조합(classifier combination)이 있음.

나. 학습 방법의 불안전성
· 학습자료의 작은 변화에 의해 예측 모형이 크게 변하는 경우, 그 학습방법은 불안정
· 가장 안정적은 방법으로는 1-nearest neighbor(가장 가까운 자료만 변하지 않으면 예측 모형이 변하지 않음), 선형회귀모형(최소제곱법으로 추정해 모형 결정)이 존재
· 가장 불안전한 방법으로는 의사결정나무가 있음
다. 앙상블 기법의 종류
1) 배깅
· 주어진 자료에서 여러 개의 붓스트랩(bootstrap) 자료를 생성하고 각 붓스트랩 자료에 예측 모형을 만든 후 결합하여 최종 예측모형을 만드는 방법
· 붓스트랩(bootstrap)은 주어진 자료에서 동일한 크기의 표본을 랜덤 복원추출로 뽑은 자료를 의미
· 보팅(voting)은 여러 개의 모형으로부터 산출된 결과를 다수결에 의해서 최종 결과를 선정하는 과정
· 최적의 의사결정나무를 구축할 때 가장 어려운 부분이 가지치기(pruning)이지만 배깅에서는 가지치기를 하지않고 최대로 성장한 의사결정나무들을 활용
· 훈련자료의 모집단의 분포를 모르기 때문에 실제 문제에서는 평균예측모형을 구할 수 없으므로 배깅은 이러한 문제를 해결하기 위해 훈련자료를 모집단으로 생각하고 평균예측모형을 구하여 분산을 줄이고 예측력을 향상

2) 부스팅
· 예측력이 약한 모형(weak learner)들을 결합하여 강한 예측모형을 만드는 방법
· 부스팅 방법 중 Adaboost는 이진분류 문제에 랜덤 분류기보다 조금 더 좋은 분류기 n개에 각각 가중치를 설정하고 n개의 분류기를 결합하여 최종분류기를 만드는 방법을 제안(단, 가중치의 합은 1)
· 훈련오차를 빨리 그리고 쉽게 줄일 수 있음
· 배깅에 비해 많은 예측오차가 향상되어 Adaboot의 성능이 배깅보다 뛰어난 경우가 많음

3) 랜덤포레스트(random forest)
· 의사결정나무의 특징인 분산이 크다는 점을 고려하여 배깅과 부스팅보다 더 많은 무작위성을 주어 약한 학습기들을 생성한 후 이를 선형 결합하여 최종 학습기를 만드는 방법
· randomForest패키지는 random input에 따른 forest of tree를 이용한 분류방법
· 랜덤한 forest에는 많은 트리들이 생성

4절 인공신경망 분석
1. 인공신경망분석(ANN)
가. 인공신경망이란?
· 생물학의 뇌는 신경세포와 신경세포를 연결하는 시냅스(synapse)를 통해서 신호를 주고 받음으로써 정보를 저장하고 학습한다. 인공신경망은 뇌의 학습 방법을 수학적으로 모델링한 기계학습 알고리즘으로써, 시냅스의 결합으로 네트워크를 형성한 신경세포가 학습을 통해 시냅스의 결합세기를 변화시켜 문제를 해결하는 모델 전반을 가리킨다.
마. 인공신경망의 특징
1) 구조

· 인공신경망은 입력층(input layer), 은닉층(hidden layer), 출력층(output layer)으로 구성되어 있다. 입력층에는 각각 입력변수가 1:1로 매칭되는 뉴런(neuron)이 존재한다.
· 은닉층에는 입력층의 뉴런과 가중치(weight)의 결합으로 생성되는 뉴런이 존재하며, 은닉층에서의 층의 개수에 따라 모형의 복잡도가 결정이 되고, 은닉층의 개수가 2개 이상이 되는 경우 deep neural network 또는 deep learning이라고 칭한다.
· 출력층에는 은닉층에서의 뉴런과 가중치가 결합하여 생성되는 뉴런이 존재하며, 예측하고자 하는 종속변수 형태에(numeric, binary or multinomial) 따라 출력층에 존재하는 뉴런은 이전층에서의 입력값과 가중치의 합(summation)을 계산하는 기능과 뉴런의 가중합을 입력값으로 신호를 출력하는 활성화 함수(activation)기능을 수행한다.

2)뉴런의 계산
· 뉴런은 전이함수, 즉 활성화 함수(activation function)를 사용
· 활성화 함수를 이용해 출력을 결정하며 입력신호의 가중치 합을 계산하여 임계값과 비교
· 가중치의 합이 임계값보다 작으면 뉴런의 출력은 -1, 같거나 크면 +1을 출력

3) 뉴런의 활성화 함수
· 시그모이드 함수의 경우 로지스틱 회귀분석과 유사하며, 0~1의 확률값을 가진다.
> # 역전파 알고리즘 : ANN(artificial neural network)을 학습시키기 위한 가장 기본적이고 일반적인 알고리즘
> # 신경망 모형의 장점
> # 변수의 수가 많거나 입력, 출력변수간에 복잡한 비선형관계에 유용
> # 잡음에 대해서도 민감하게 반응하지 않는다.
> # 연속형이거나 이산형인 경우 모두 처리가 가능
> # 신경망 모형의 단점
> # 결과에 대한 해석이 쉽지 않다.
> # 최적의 모형을 도출하는 것이 상대적으로 어렵다.
> # 데이터의 정규화를 하지 않으면 지역해에 빠지기 쉽다.
> # 모형이 복잡하면 훈련 과정에 시간이 많이 소요된다.
> data(iris)
> #scale()함수를 이용해서 정규화를 한다.
> iris
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
7 4.6 3.4 1.4 0.3 setosa
8 5.0 3.4 1.5 0.2 setosa
9 4.4 2.9 1.4 0.2 setosa
10 4.9 3.1 1.5 0.1 setosa
.....
139 6.0 3.0 4.8 1.8 virginica
140 6.9 3.1 5.4 2.1 virginica
141 6.7 3.1 5.6 2.4 virginica
142 6.9 3.1 5.1 2.3 virginica
143 5.8 2.7 5.1 1.9 virginica
144 6.8 3.2 5.9 2.3 virginica
145 6.7 3.3 5.7 2.5 virginica
146 6.7 3.0 5.2 2.3 virginica
147 6.3 2.5 5.0 1.9 virginica
148 6.5 3.0 5.2 2.0 virginica
149 6.2 3.4 5.4 2.3 virginica
150 5.9 3.0 5.1 1.8 virginica
> iris.scaled<-cbind(scale(iris[-5]),iris[5])
> # 데이터를 training set과 test set으로 분할
> idx<-c(sample(1:50,35),sample(51:100,35),sample(101:150,35))
> train<- iris.scaled[idx,]
> test<-iris.scaled[-idx,]
> library(nnet)
> #size(은닉층)
> model.nnet<-nnet(Species~.,data=train,size=2,decay=5e-04)
# weights: 19
initial value 115.278951
iter 10 value 37.113811
iter 20 value 10.838166
iter 30 value 7.080931
iter 40 value 6.671625
iter 50 value 6.444395
iter 60 value 6.346762
iter 70 value 6.179517
iter 80 value 6.126565
iter 90 value 6.025450
iter 100 value 6.017144
final value 6.017144
stopped after 100 iterations
> summary(model.nnet)
a 4-2-3 network with 19 weights
options were - softmax modelling decay=5e-04
b->h1 i1->h1 i2->h1 i3->h1 i4->h1
2.72 1.01 -2.64 4.02 3.47
b->h2 i1->h2 i2->h2 i3->h2 i4->h2
-4.02 -0.52 -0.56 3.76 2.66
b->o1 h1->o1 h2->o1
6.02 -8.85 -4.21
b->o2 h1->o2 h2->o2
-2.16 8.72 -7.25
b->o3 h1->o3 h2->o3
-3.85 0.28 11.49
> pred <-predict(model.nnet,test,type="class")
> pred
[1] "setosa" "setosa" "setosa" "setosa" "setosa" "setosa" "setosa" "setosa"
[9] "setosa" "setosa" "setosa" "setosa" "setosa" "setosa" "setosa" "versicolor"
[17] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[25] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor" "versicolor" "virginica" "virginica"
[33] "virginica" "virginica" "virginica" "virginica" "virginica" "virginica" "virginica" "virginica"
[41] "virginica" "virginica" "virginica" "virginica" "virginica"
> # 오분류표 : 실제결과와 예측결과에 대한 교차표
> # table함수를 이용한다.
> actual <- test$Species
> table(actual, pred)
pred
actual setosa versicolor virginica
setosa 15 0 0
versicolor 0 15 0
virginica 0 0 15바. 신경망 모형 구축시 고려사항
1) 입력변수
연속형 변수 : 입력변수 값들의 범위가 변수간의 큰 차이가 없을때 |
· 연속형 변수인 경우
범주화 : 각 범주의 빈도가 비슷하게 되도록 설정 |
2) 가중치의 초기값과 다중 최소값 문제
· 역전파 알고리즘은 초기값에 따라 결과가 많이 달라지므로 초기값의 선택은 매우 중요한 문제
· 가중치가 0이면 시그모이드 함수는 선형이되고 신경망 모형은 근사적으로 선형모형이 됨
· 일반적으로 초기값은 0근처로 랜덤하게 선택하므로 초기모형은 선형모형에 가깝고, 가중치 값이 증가할수록 비선형 모형이 된다.(초기값이 0이면 반복하여 값이 전혀 변하지 않고,너무 크면 좋지 않은 해를 주는 문제점을 내포하고 있으므로 주의 필요)
4) 은닉층(hidden alyer)과 은닉노드(hidden node)의 수
· 은닉층과 은닉노드가 많으면 가중치가 많아져서 과대적합 문제 발생
· 은닉층과 은닉노드가 적으면 과소적합 문제 발생
· 은닉층의 수가 하나인 신경망은 범용 근사자(universal approximator)이므로 매끄러운 함수를 근사적으로 표현. 그러므로 은닉층은 하나로 선정
· 은닉노드의 수는 적절히 큰 값으로 놓고 가중치를 감소(weight decay)시키며 적용하는 것이 좋음
5) 과대 적합 문제
· 신경망에서는 많은 가중치를 추정해야 하므로 과대적합문제가 빈번
· 알고리즘의 조기 종료와 가중치 감소기법으로 해결
· 모형이 적합하는 과정에서 검증오차가 증가하기 시작하면 반복을 중지하는 조기종료를 시행
· 선형모형의 능형회귀와 유사한 가중치 감소라는 별점화 기법을 활용
5절 군집분석
1. 군집분석
가. 개요
· 각 객체에 대해 관측된 여러개의 변수 값들로부터 n개의 개체를 유사한 성격으로 군집화하고 형성된 군집들의 특성을 파악하여 군집들 사이의 관계를 분석하는 다변량 분석기법
· 별도 반응 변수 필요 없음
· 개채 간의 유사성에만 기초하여 군집형성
· 이상값 탐지에도 사용, 심리학, 사회학, 경영학, 생물학등 다양한 분야 이용
· 계층적 군집, 분리 군집, 밀도-기반군집, 모형-기본군집, 격자-기반군집, 커널-기반군집, SOM 사전에 그룹을 알지 못함 → 분석을 통해 나중에 자동적으로 분류(사전에 그룹을 알면 분류)
2.거리
가. 맨하탄(Manhattan) 거리 : 유클라디안 거리와 함께 가장 많이 사용되는 거리로 맨하탄 도시에서 건물에서 건물을 가기위한 최단 거리를 구하기 위해 고안된 거리

나. 범주형 변수의 경우
· 코사인 유사도 : 두 개체 백터 내적의 코사인 값을 이용하여 측정된 벡터간의 유사한 정도

3. 계층적 군집분석
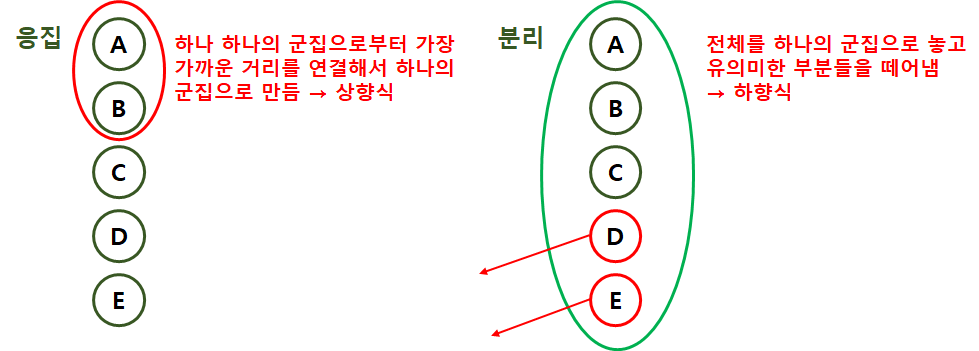
※ 계층적 군집
· 각 데이터 데이터 수만큼 n개의 독립군집에서 출발하여 점차 거리가 가까운 대상과 군집을 이루어 가는 것
· R에서 계층적 군집을 수행할 때
① 병합적 방법을 사용하는 함수 : hclust, cluster 패키지의 agnes(), mclust()
② 분할적 방법을 사용하는 함수 : cluster 패키지의 diana(), mona()
* 수학적 거리 : 유클리드, 맨하튼, 민코프스키
* 통계적거리 : 표준화거리, 마할라노베스
* H-cluster에서 군집을 지정해 주는 방법

가. 최단연결법
⋅ n*n 거리행렬에서 거리가 가장 가까운 데이터를 묶어서 군집을 형성
⋅ 군집과 군집 또는 데이터와의 거리를 계산시 최단거리(min)를 거리로 계산하여 거리 행렬 수정을 진행
⋅ 수정된 거리행렬에서 거리가 가까운 데이터 또는 군집을 새로운 군집을 형성

나. 최장연결법

다. 평균연결법(average linkage)
· 군집과 군집 또는 데이터와의 거리를 계산할 때 평균(mean)을 거리로 계산하여 거리행렬을 수정하는 방법
라. 와드 연결법(ward linkage)
· 군집내 편차들의 제곱하을 고려한 방법
· 군집 간 정보의 손실을 최소화하기 위해 군집화를 진행
> #H-Clustering
> a<-1:8
> a
[1] 1 2 3 4 5 6 7 8
> dim(a)<-c(2,4)
> a
[,1] [,2] [,3] [,4]
[1,] 1 3 5 7
[2,] 2 4 6 8
> class(a)
[1] "matrix"
> #matrix(벡터,nrow,ncol)
> matrix(1:8,nrow=2,ncol=4,byrow=TRUE)
[,1] [,2] [,3] [,4]
[1,] 1 2 3 4
[2,] 5 6 7 8
> d<-matrix(c(0,1,11,5,8,
+ 1,0,2,3,4,
+ 11,2,0,4,5,
+ 5,3,4,0,6,
+ 7,5,6,12,0),nrow=5,ncol=5)
> d
[,1] [,2] [,3] [,4] [,5]
[1,] 0 1 11 5 7
[2,] 1 0 2 3 5
[3,] 11 2 0 4 6
[4,] 5 3 4 0 12
[5,] 8 4 5 6 0
> #거리(자신의 거리는 제외)
> d<-as.dist(d)#거리 행렬 만들기 as.dist함수
> d
1 2 3 4
2 1
3 11 2
4 5 3 4
5 8 4 5 6
> hclust(d,method="single")#single linkage 최단 연결법
Call:
hclust(d = d, method = "single")
Cluster method : single
Number of objects: 5
> plot(hclust(d,method="single"))
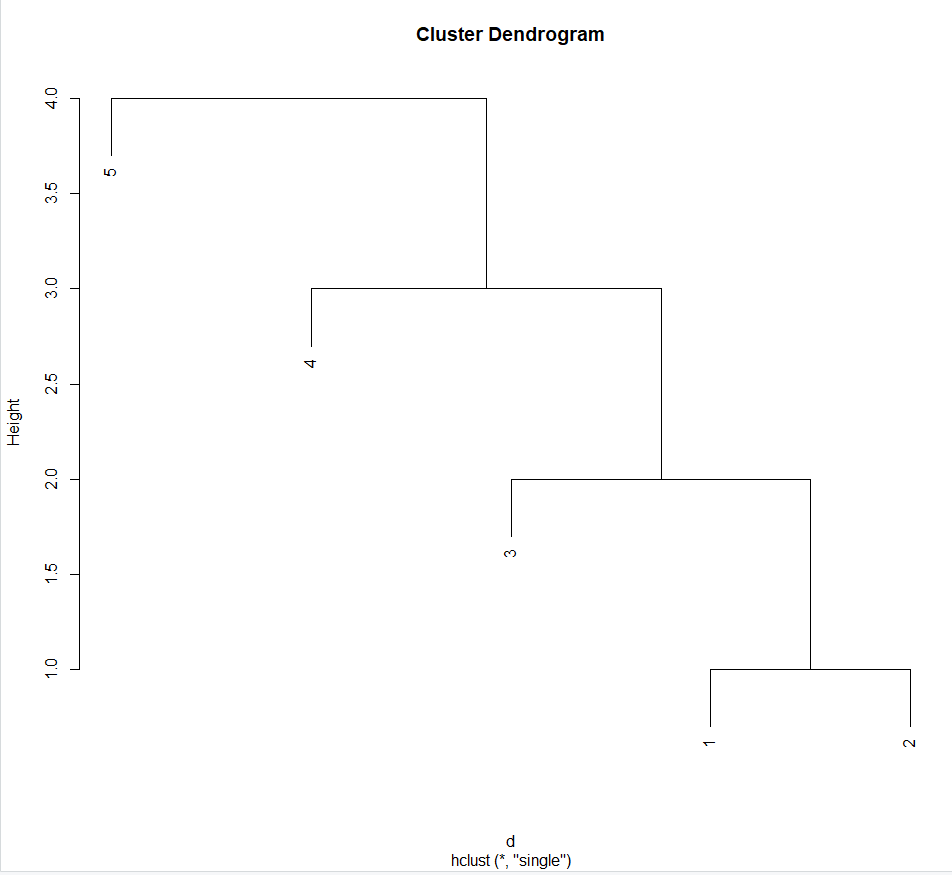
> #평균연결법 : 모든 항목에 대한 거리 평균을 구하면서 군집하는 방법
> # 계산량이 불필요하게 많아짐
> #중심연결법 : 두개의 군집의 중심간의 거리를 측정한다. 두군집 결합했을때 새로운
> # 군집의 평균을 이용해서 중심을 구하고, 그 중심과 또다른 군집의 중심
> # 사이의 거리를 측정하여 최소거리를 찾아 군집을 이룬다.
> #와드 연결법 : 군집 내의 오차제곱합에 기초하여 군집을 수행
> #1과 2가 묶이고 3이 묶이고 4가 묶이고 마지막으로 5가 묶임
> plot(hclust(d,method="complete")) #complete linkage 최장연결법

> plot(hclust(d,method="average")) #average linkage 평균연결법

plot(hclust(d,method="centroid")) #centroid 중심 연결법

> plot(hclust(d,method="ward.D2")) #ward linkage 와드 연결법법

4. 비계층적 군집분석
· 사전에 군집수를 정해주어 대상들이 군집에 할당되도록 하는것
가. K-평균 군집분석(k-means clustering)의 개념
· 주어진 군집수 k에 대해서 군집내 거리의 제곱합의 합을 최소화 하는 것을 목적으로 함. 즉, 군집내 거리 제곱합이 얼마나 군집화가 잘 되었는지를 알려주는 척도
나. K-평균 군집분석(K-means clustering)과정
· 원하는 군집의 개수와 초기 값(seed)들을 정해 seed 중심으로 군집을 형성
· 각 데이터를 거리가 가장 가까운 seed가 있는 군집으로 분류
· 각 군집의 seed 값을 다시 계산
· 모든 개체가 군집으로 할당될 때까지 위 과정들을 반복

다. K-평균 군집분석의 특징
| 장점 | 단점 |
· 다양한 형태의 데이터에 적용이 가능 |
· 군집수 k가 원데이터 구조에 적합하지 않으면 좋은 결과를 얻을 수 없음 |
> #비계층적 군집
> x<-matrix(rnorm(100),nrow=5)
> x
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] 1.0826110 0.89870272 -0.27007961 0.3301416 -0.7642599 0.5624718 1.8912270 1.913059422
[2,] -0.9526855 -0.51874236 1.61978988 0.9553246 -2.3445134 -0.7837751 -0.8780771 -0.005234058
[3,] 1.1264827 0.55443855 -0.21413117 1.1439599 -0.4716834 -0.2260540 -0.1125589 -0.152260049
[4,] -0.6490430 -0.08797367 -0.81778246 0.1005224 -0.5158555 -1.5871030 1.9487131 -0.509631657
[5,] 0.2924701 -1.13521293 -0.05402292 1.1645752 -2.3160362 0.5475242 0.9338163 1.434573703
[,9] [,10] [,11] [,12] [,13] [,14] [,15] [,16]
[1,] -1.28583853 -1.5092882 -0.2755247 -2.6517412 0.9825054 -3.3960635 0.45709951 0.03615287
[2,] 0.30731422 0.2326318 -0.6787586 -0.5805822 0.3157640 -0.7813523 0.53883312 -0.42139311
[3,] -0.04631853 -0.0396487 0.5008359 1.4541869 -1.5070626 1.1024646 0.01464312 -0.89936441
[4,] 2.25184180 -0.8391251 -0.3316623 0.8381294 0.2055698 0.5287450 -0.91648914 0.41744132
[5,] -0.60803373 0.1322911 -1.8349803 1.2150536 1.5972281 0.7893944 -1.22681509 0.15344474
[,17] [,18] [,19] [,20]
[1,] 1.46328305 -0.2847059 1.1330102 0.3741440
[2,] -1.12150250 -0.7081712 -0.6040689 -0.1060861
[3,] -0.51778808 -2.1476390 0.5575116 0.1660620
[4,] -0.07494709 -0.2838372 0.1426293 0.6580348
[5,] -1.40779008 -0.5340722 -1.2368602 0.1139629
> dist(x)
1 2 3 4
2 7.307738
3 8.136763 5.501379
4 7.841817 5.763214 5.309413
5 8.020636 5.043075 6.004192 5.834316
> #수학적 거리, 통계적 거리
> # dist() 함수는 유클리드(euclidean)거리가 Default 값이다.
> #맨하탄거리,민콥스키거리
> #통계적 기리 :표준화거리, 마할라 노비스
> dist(x,method="manhattan")
1 2 3 4
2 28.43765
3 26.99321 20.54399
4 25.39765 21.46821 20.18287
5 26.97468 18.82964 21.32580 22.15528
> dist(x,method="minkowski")
1 2 3 4
2 7.307738
3 8.136763 5.501379
4 7.841817 5.763214 5.309413
5 8.020636 5.043075 6.004192 5.834316
> data(iris)
> head(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
> # iris의 Species 별로 잘 나누어지는지 알아봄
> # kmeans() 함수를 이용하여 비계층적 군집을 함
> kmeans.iris<-kmeans(iris[-5],3)
> #군집 내 제곱합의 합을 최소화 하는것이 목표이므로 그값을 구함
> #소숫점 둘째짜리 까지 반올림함
> sum(kmeans.iris$withinss)
[1] 142.7535
> #withiss 군집내에 있는 객체간 제곱합의 벡터
> kmeans.iris$tot.withinss
[1] 142.7535
> round(kmeans.iris$tot.withinss,2)
[1] 142.75
> #r군집화 확인
> kmeans.iris$cluster
[1] 2 3 3 3 2 2 2 2 3 3 2 2 3 3 2 2 2 2 2 2 2 2 2 2 3 3 2 2 2 3 3 2 2 2 3 2 2 2 3 2 2 3 3 2 2 3 2 3 2 2 1
[52] 1 1 1 1 1 1 3 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 3 1 1 1 1 3 1 1 1
[103] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
> iris[,5]
[1] setosa setosa setosa setosa setosa setosa setosa setosa setosa
[10] setosa setosa setosa setosa setosa setosa setosa setosa setosa
[19] setosa setosa setosa setosa setosa setosa setosa setosa setosa
[28] setosa setosa setosa setosa setosa setosa setosa setosa setosa
[37] setosa setosa setosa setosa setosa setosa setosa setosa setosa
[46] setosa setosa setosa setosa setosa versicolor versicolor versicolor versicolor
[55] versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor
[64] versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor
[73] versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor
[82] versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor
[91] versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor
[100] versicolor virginica virginica virginica virginica virginica virginica virginica virginica
[109] virginica virginica virginica virginica virginica virginica virginica virginica virginica
[118] virginica virginica virginica virginica virginica virginica virginica virginica virginica
[127] virginica virginica virginica virginica virginica virginica virginica virginica virginica
[136] virginica virginica virginica virginica virginica virginica virginica virginica virginica
[145] virginica virginica virginica virginica virginica virginica
Levels: setosa versicolor virginica
> table(iris[,5],kmeans.iris$cluster)
1 2 3
setosa 0 33 17
versicolor 46 0 4
virginica 50 0 0
> #10번 더 실행
> kmeans10.iris<-kmeans(iris[-5],3,nstart=10)
> table(iris[,5],kmeans10.iris$cluster)
1 2 3
setosa 0 50 0
versicolor 48 0 2
virginica 14 0 365. 혼합군포군집(mixture distribution clustering)
가. 개요
· 모형 기반(model-based)의 군집 방법이며, 데이터가 k개의 모수적 모형(흔히 정규분포 또는 다변량 정규분포를 가정함)의 가중합으로 표현되는 모집단 모형으로부터 나왔다는 가정하에서 모수와 함께 가중치를 자료로부터 추정하는 방법
· K개 각 모형은 군집을 의미하며, 각 데이터는 추정된 k개의 모형 중 어느 모형으로부터 나왔을 확률이 확률이 높은지에 따라 군집의 분류가 이루어짐.
· 흔히 혼합모형에서의 모수와 가중치의 추정(최대가능도추정)에는 EM알고리즘이 사용
· 장점: 확률분포를 도입하여 군집수행하는 모형기반 군집방법으로, 군집을 몇 개의 모수로 표현할 수 있고, 서로 다른 크기나 모양의 군집을 찾을 수 있음.
· 단점 : EM알고리즙을 통한 모수 추정에 시간이 걸리고, 군집크기가 작으면 추정도가 저하되어 어렵다. 또한 이상값에 민감하여 사전에 제거해줘야 한다.
다. EM(Expectation-Maximization) 알고리즘의 진행과정
· E단계 : 각 집단의 분포는 정규 분포를 따른다고 가정하고, 각 자료가 어느 집단에서 나온지 안다면 해당모수의 추정은 어렵지 않다. 그러나, 각 자료가 어느집단에서 나온지 모르니까 잠재변수의 개념을 도입하게 된다. 잠재변수가 2 일 때, 모수 초기값이 주어져 있다면(초기 분포값을 안다면), 각 자료가 어느 집단으로부터 나올 확률이 높은지에 대해 추정할 수 있다.
· M단계 : 그 다음 각 자료의 x의 조건분포로부터 조건부 기대값을 구한다. 관측변수 x와 잠재변수 2를 포함하는 로그 가능도 함수에 상수값인 2의 조건부 기댓값을 대입하여, 로그 가능도 함수를 최대로 하는 모수를 찾는다.
n1<-rnorm(50,0,2)
n2<-rnorm(50,8,2)
mixdata<-c(n1,n2)
hist(mixdata,breaks=20,main="혼합 분포히스토그램램")

6. SOM(Self Organizing Map : 자기조직화지도)
가. 개요
· 두 개의 인공신명망 구조로 변수와 동일하게 뉴런수가 존재하며, 자료는 학습을 통해 경쟁층에(맵) 정렬하게 된다. 입력층은 입력벡터를 받는 층이고, 경쟁층은 2차원 격자구조로 입력 벡터의 특성에 따라 벡터가 한점으로 클러스터링 되는 층이다. 또한 입력층의 뉴런들은 경쟁층에 각각의 뉴런과 연결되는 완전 연결의 형태를 말한다.
· SOM은 비지도 신경망으로 고차원의 데이터를 이해하기 쉬운 저차원의 뉴런으로 정렬하여 지도의 형태로 형상화
· 입력변수의 위치관계를 그대로 보존한다는 특징이 있다. 다시 말해 실제 공간의 입력변수가 가까이 있으면, 지도상에도 가까운 위치에 있게 된다.(패턴발견이나, 이미지분석에 용이)
나. 구성
· 입력층(input layer) : 입력벡터를 받는 중
· 경쟁층(competitive layer) : 입력벡터 특성에 따라 입력벡터가 한점으로 클러스터링 되는 층
· 가중치(weight) : 인공신경망에서 가중치는 각 입력값에 대한 입력값의 중요도 값을 의미
· 노드(node) : 경쟁층에서 입력벡터들이 서로의 유사성에 의해 모이는 하나의 영역

다. 특징
· 구조탐색 : 데이터의 특징을 파악하여 유사데이터를 clustering 한다. 고차원의 데이터 셋을 저차원인 맵(2D 그리드에 매칭)에 표현하는 것인데 이를 통해 SOM은 입력데이터를 유사한 그룹으로 분류한다.
· 차원축소 & 시각화 : 차원을 축소하여 통상 2차원 그리드에 매핑하여 인간이 시각적으로 인식할 수 있게 한다.
라. SOM과 신경망 모형의 차이점
| 구분 | 신경망 모형 | SOM |
| 학습방법 | 오차역전파법 | 경쟁학습방법 |
| 구성 | 입력층, 은닉층, 출력층 | 입력층, 2차원 격자(grid) 형태의 경쟁층 |
| 기계학습 방법의 분류 | 지도학습(Supervised Learning) | 비지도 학습(Unsupervised Learning) |
| 연속적인 layer | 2차원그리드 | |
| 에러 수정을 학습 | 경쟁학습 |
7. 최신 군집분석 기법들
· R에서 SOM 구현을 위한 패키지
· Kohonen 패키지, SOM 함수
6절 연관분석
1. 연관규칙
가. 연관규칙분석(Association Analysis) 개념
· 항목들간의 '조건-결과' 식으로 표현되는 유용한 패턴을 말한다. 이러한 패턴, 규칙을 발견해 내는것을 연관분석이라 하며, 흔히 장바구니 분석이라고도 한다.
· 장바구니 분석 : 우유를 살때 빵을 얼마나 살지
다. 연관규칙의 측도(측정지표)
· 지지도, 신뢰도, 향상도
1) 지지도(support)
· 전체 거래 중 항목 A와 항목 B를 동시에 포함하는 거래의 비율로 정의


2) 신뢰도(confidence)
· 항목 A를 포함한 거래 중에서 항목 A와 항목 B가 같이 포함될 확률

3) 항상도(Lift)
· 상품 A를 구매한 사람이 B를 구매할 확률과 A의 구매와 상관없이 B를 구매할 확률의 비율
· A가 구매되지 않았을 때 품목 B의 구매확률에 비해 A가 구매됐을 때 품목 B의 구매확률의 증기 비
· 연관규칙 A→B는 품목 A와 품목 B의 구매가 서로 관련이 없는 경우에 향상도가 1이 됨
· 즉, A와 B가 관련성이 없다면 Lift=1이 되고, Lift>1면 Lift 값이 클수록 관련도가 높다. Lift<1면 오히려 A를 구매한 사람은 B를 구매하지 않는다는 결론이 나온다.

라. 연관규칙의 절차
· Apriori(우유 구매 고객이 빵을 구매하는 패턴) 알고리즘 분석절차
- 최소지지도를 설정
- 개별품목중에서 최소 지지도(A를 B를 동시에 구매할 확률/전체거래)를 넘는 모든 품목을 찾음
- 찾은 개별품목만을 이용하여 최소지지도를 넘는 두가지 품목 집합을 찾음
- 찾은 품목집합을 결합하여 최소지지도를 넘는 세가지 품목집합을 찾음
- 반복적으로 수행하여 최소 지지도가 넘는 빈발 품목을 찾음
· 절차
① 최소지지도 결정 → ② 품목 중 최소 지지도를 넘는 품목 분류 → ③ 2가지 품목 집합 생성 → ④ 반복적으로 수행해 빈발품목 집합을 찾음
마. 연관규칙의 장점과 단점
| 장점 | 단점(개선방안) |
· 변수의 개수가 많은 경우에 쉽게 사용할 수 있음 |
· 거래가 드문 품목에 대한 정보를 찾기 어려움 |
바. 순차패턴(Sequence Analysis)
· 동시에 구매될 가능성이 큰 상품군을 찾아내는 연관성분석에 시간이라는 개념을 포함시켜 순차적으로 구매 가능성이 큰 상품군을 찾아내는 것
· 연관성분석에서의 데이터 형태에서 각각의 고객으로부터 발생한 구매시점에 대한 정보가 포함

'ADSP' 카테고리의 다른 글
| PART 03 데이터 분석 - 2 (0) | 2020.03.06 |
|---|---|
| PART 03 데이터 분석 - 1 (0) | 2020.02.24 |
| PART 02. 데이터 분석 기획 (0) | 2020.02.23 |
| PART 01. 데이터 이해 (0) | 2020.02.22 |
| [ADSP] R Studio설치 (0) | 2020.01.21 |



