4장 통계분석
1절 통계분석의 이해
1. 통계
· 특정집단을 대상으로 수행한 조사나 실험을 통해 나온 결과에 대한 요약된 형태의 표현
· 통계학
- 자료의 수집, 정리, 해석 이 세가지가 통계학의 핵심 (Data -----statistic-----> Information)
· 기술 통계학 : 수집된 정보를 정리하고 요약(운동선수 기록)
· 추론 통계학 : 수집된 정보를 통해 예측(출구조사) → 확률론(불확실성 내포)
· 조사대상에 따라 총조사(census)와 표본조사로 구분
2. 통계자료의 획득 방법
가. 총 조사/전수 조사(census)
나. 표본조사
· 모집단이 클 경우 사용
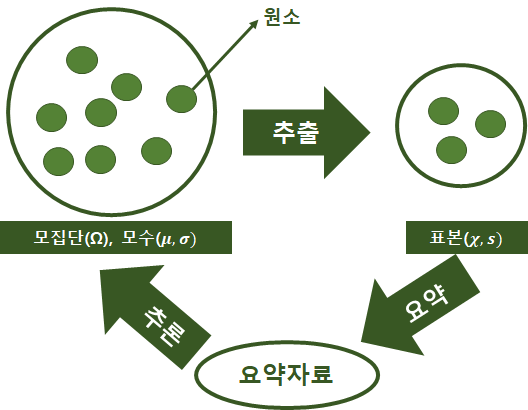
· 모집단(population) : 조사하고자 하는 대상 집단 전체
· 원소(element) : 모집단을 구성하는 개체
· 표본(sample) : 모집단의 일부 원소, 부분집합(모집단의 일부원소)
· 모수(parameter) : 모집단에 대한 정보( 모집단의 속성, 특징을 나타내는 통계값 : 모평균, 모표준편차, 모상관계수)
· 모집단의 정의, 표본의 크기, 조사방법, 조사기간, 표본 추출방법을 정확히 명시
· 통계량 : 표본의 평균/ 표준편차/ 상관계수
다. 표본 추출 방법
· 모집단을 대표할 수 있는 표본 추출
1) 단순랜덤 추출법(simple random sampling)
· 임의의 n개를 추출하는 방법
· 각 샘플은 선택될 확률이 동일(비복원, 복원(추출한 element를 다시 집어넣어 추출하는 경우) 추출)
2) 계통추출법(systematic sampling)
· 모집단이 클 경우 사용
· 모집단의 개체에 1, 2, · · ·,N 이라는 일련번호를 부여한 후, 첫 번째 표본을 임의로 선택하고 일정간격으로 다음 표본을 선택

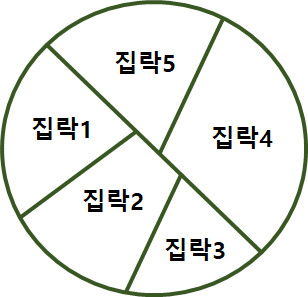
3) 집락추출법(cluster random sampling)
· 조사지역이 너무 넓은 경우
· 군집을 구분하고 군집별로 단순랜덤 추출법(지역표본추출, 다단계표본추출)
4) 층화추출법(stratified random sampling)
· 이질적인 원소들로 구성된 모집단에서 각 계층을 고루 대표할 수 있도록 표본을 추출
· 사용자 만족도 100명 → 남 : 여 = 7 : 3 → 남여비율 7:3으로 추출
◎ 비확률표본 추출
1) 판단추출법 : 연구자가 연구목적에 따라 판단하여 표본 선택
→ 제한된 집단으로 연구
- 장점 : 비용/시간 단축
- 단점 : 대표성 보장없음
2) 할당추출법 : 모집단의 속성을 많이 반영하는 추출법. 모집단 특성의 비율에 맞춰 표본 추출 분류자의 판단이 들어가서 오차에 대한 개입가능성
- ex) 대학교 만족도 조사(500명)
→ 100명 추출 : 학과별로 인원수 다름(학과별 인원수 비율 반영)
3) 편의 추출법 : 손쉽게 표본 추출. 연구자가 쉽게 접근할 수 있는 표본 추출 표본이 모집단을 대표하지 않음. 사회과학에서 많이 사용.
4) 지원자 표본 추출법 : 지원자를 표본으로 추출
라. 측정(measurement)
1) 개요
· 어떤 특정한 현상을 관찰하여 어떤 일정한 규칙에 의해 수치 부여
2) 측정방법
| 명목척도 | · 측정대상의 특성만 구분하기위해 숫자, 기호할당(양적인 분석X, 대소비교X) | 질적척도 (범주형자료, 숫자들의 크기 차이가 계산되지 않는 척도) | |
(서열척도) | · 상대적으로 크기 O, 서로간 비교가능 → 크기의 정도를 알 수 X(사칙연산X) | ||
(등간척도) | · 명목척도, 서열척도 특성모두 가지고 있음(+, - 기능 / ×, ÷ 불가능) → 0이 없음. 절대 0점이 아니다) | 양적척도 (수치형 자료, 숫자들의 크기차이를 계산할 수 있는 척도) | |
| 비율척도 | · 가장 높은 수준의 척도 | ||
· 구간척도는 절대적 크기는 측정할 수 없기 때문에 사칙연산 중 더하기와 뺴기는 가능하지만 비율처럼 곱하거나 나누는 것은 불가능
3. 통계분석
가. 정의
· 특정한 집단이나 불확실한 현상을 대상으로 자료를 수집해 대상 집단에 대한 정보를 구하고, 적절한 통계분석 방법을 이용해 의사결정을 하는 과정(통계적 추론)
나. 기술통계(descriptive statistics)
· 수집된 자료를 정리 요약 하기 위해 사용되는 기초 통계(자세한 통계 분석을 위한 전단계 역할)
다. 통계적 추론(추측통계, inference statistics)
· 수집된 자료를 이용해 대상집단(모집단)에 대한 의사결정을 하는 것
1) 모수 추정
·모집단의 특성인 모수(평균, 분산 등)를 분석
2) 가설검정
· 옳은지 그른지에 대한 채택여부를 결정
3) 예측
· 불확실성을 해결해 효율적인 의사결정
4. 확률 및 확률분포
가. 확률
· 특정사건에 일어날 가능성의 척도
1) 표본공간(sample space, Ω)
· 나타날 수 있는 모든 결과들의 집합
2) 사건(event)
· 표본공한의 부분집합
3) 원소(element)
· 나타날 수 있는 개별의 결과들을 의미
4) 확률변수(random variable)
· 특정값이 나타날 가능성이 확률적으로 주어지는 변수
· 정의역(domain)이 표본공간, 치역(range)이 실수값(0<y<1)인 함수
· 이산형 확률변수(discrete random variable), 연속형 확률변수(continuous random variable)
· 확률변수의 기대값

◎ 이산확률 변수의 기댓값(→평균)
- 100명 중 추출
| 점수 | 30 | 40 | 50 |
| 학생수 | 2 | 3 | 1 |
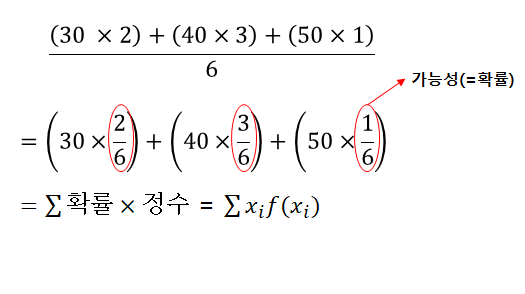
| X | 0 | 1 | 2 |
| f(X) | 1/4 | 1/2 | 1/4 |
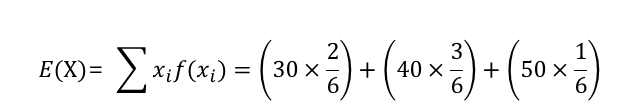
· 확률변수X의 k차 적률(k-th moment)

· 확률변수 X의 k차 중심 적률(k-th cental moment)
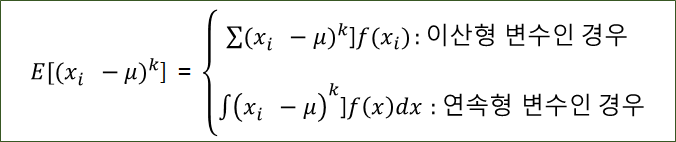
· 2차 중심적률

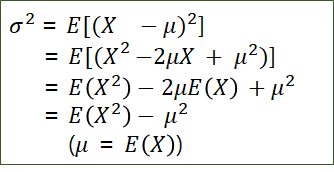
· 모분산 = 2차적률 - 1차적률^2로 해석
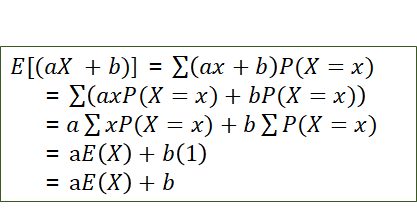
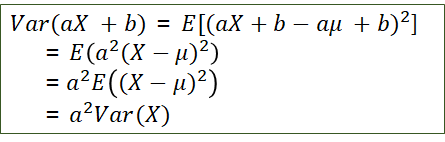
· 종속사건
- A : 홀수가 일어날 확률 (1, 3, 5)
- B : 짝수가 일어날 확률 (2, 4, 6)
- A가 발생했을 경우 B의 사건은 일어나지 않음.
· 독립사건 : 확률에 영향을 미치지 않음

· 배반사건 : 교집합 X
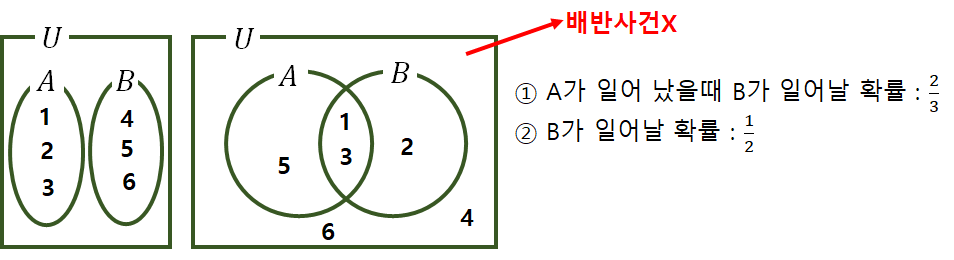
· 조건부 확률과 독립사건
→ 확률이 0이 아닌 사건 A가 일어났을 때 사건 B가 일어날 확률은 사건 A가 일어 났을 때의 사건 B의 조건부확률이라 하고 P(B | A)와 같이 나타 낸다.
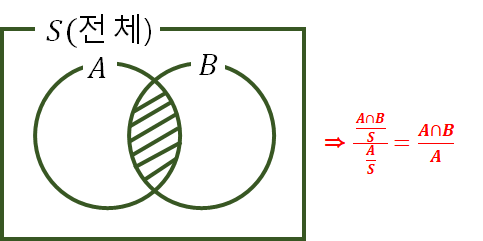
· 조건부 확률 계산
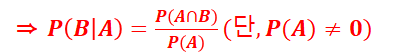
· 한개의 주사위를 던져서 홀수의 눈이 나왔을 때 그것이 소수일 확률을 구하여라.
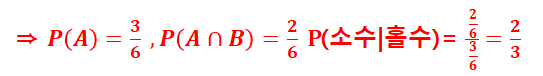
· 독립사건
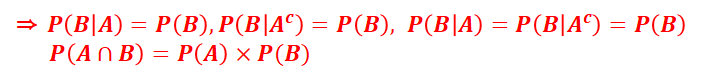
나. 확률 분포
1) 이산형 확률변수
· 동전 2개 앞면이 나올 확률 (이산확률분포표)
| X | 0 | 1 | 2 |
| P(X) | 1/4 | 1/2 | 1/4 |
→ 확률질량함수 : 이산확률 분포의 확률함수

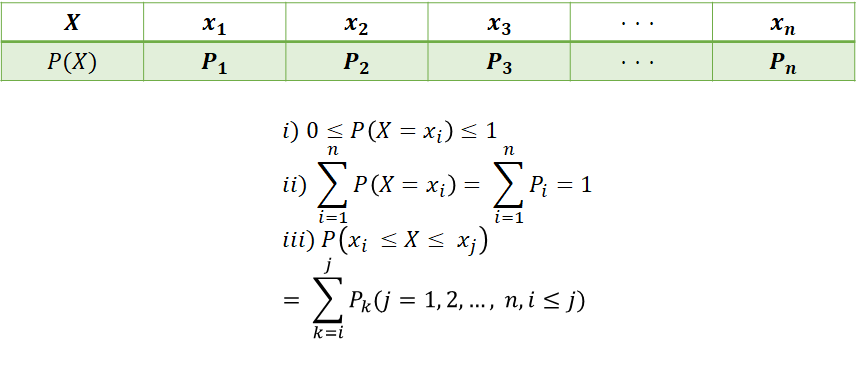
· 주사위 1개
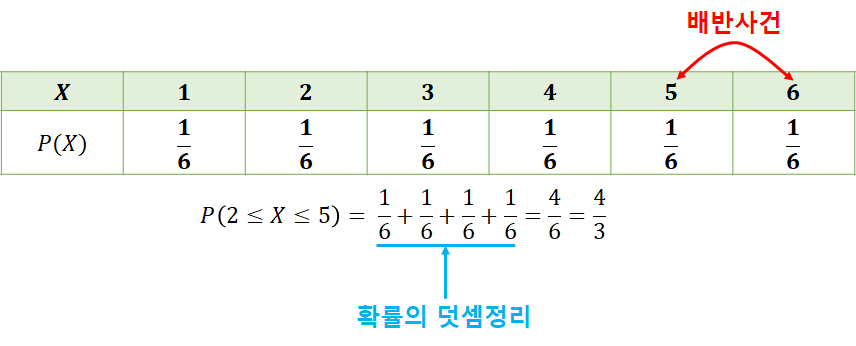
가) 베르누이 확률분포
| X | P(X) | |||
| 시행 | 성공(특정 사건 발생) | 1 | p | |
| 실패(특정 사건 발생 X) | 0 | 1-p | ||
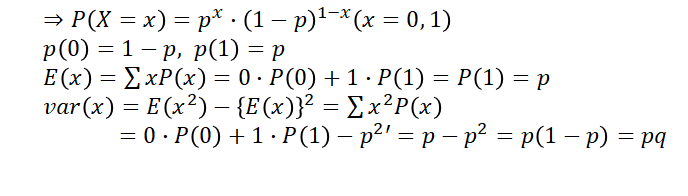
나) 이항 분포(Binomial distribution)
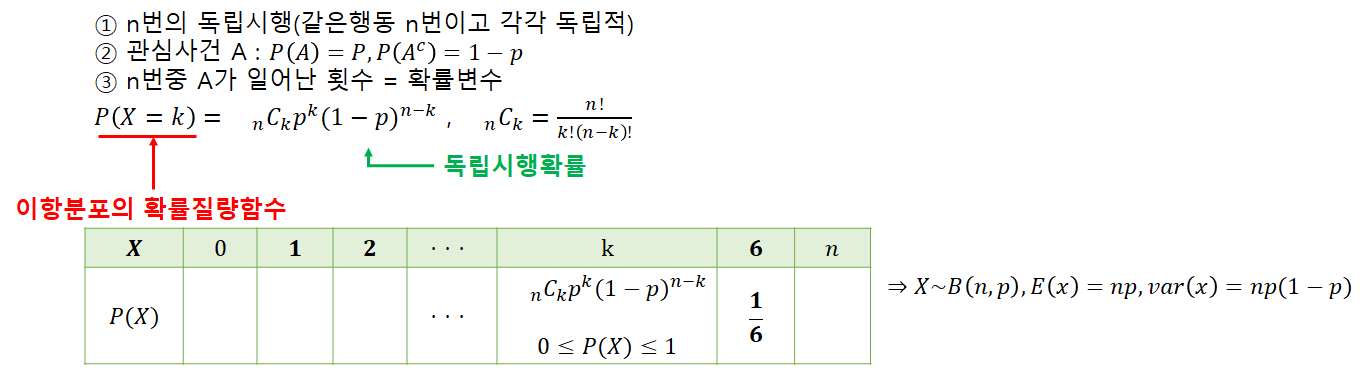
다) 기하분포(Geometric distribution)
· 성공확률이 p인 베르누이 시행에서 첫번째 성공이 있기까지 x번 실패할 확률
라) 다항분포(Multinomial distribution)
· 이항분포를 확장한 것으로 세가지 이상의 결과를 가지는 반복시행에서 발생하는 확률분포
마) 포아송분포(Poisson distribution)
· 시간과 공간 내에서 발생하는 사건의 발생횟수에 대한 확률분포(예 : 책에 오타가 5page당 10개씩 나올경우 한페이지에 오타가 3개 나올확률)
2)연속형 확률변수
· 가능한 값이 실수의 어느 특정구간 전체에 해당하는 확률변수(확률 밀도 함수)
가) 균일 분포(일양분포, Unifrom distribution)
· 모든 확률변수 X가 균일한 확률을 가지는 확률분포(다트의 확률분포)
나)정규분포(Normal distribution)

다) 지수분포(Exponential distribution)
· 어떤 사건이 발생할 때까지 경과시간에 대한 연속 확률분포
ex) 전자레인지 수명시간, 콜센터에 전화가 걸려올 때까지의 시간, 은행에 고객이 내방하는데 걸리는 시간, 정류소에 버스가 올때까지의 시간
라) t-분포(t-distribution)
· 표준정규분포와 같이 평균이 0을 중심으로 좌우가 동일한 분포를 따름
· 데이터가 연속형일 경우 사용
· 표본이 커져서(30개 이상) 자유도가 증가하면 표준정규분포와 거의 같은 분포
· 두 집단의 평균이 동일한지 알고자 할 때 검정통계량으로 활용
마) x^2-분포(chi-square distribution)
· 모평균과 모분산이 알려지지 않은 모분산에 가설검정에 사용되는 분포
· 두 집단간의 동질성 검정에 활용(범주형 자료에 대해 얻어진 관측값과 기대값의 차이를 보는 적합성 검정에 활용)
바) F-분포(F-distribution)
· 두집단간의 분산의 동일성 검정에 사용
· 확률변수는 항상 양의 값만을 갖고 x^2분포와 달리 자유도를 2개 가지고 있으며 자유도가 커질수록 정규분포에 가까워짐
5. 추정과 가설검정
가. 추정의 개요
1) 확률표본(random sample)
· 확률분포는 분포를 결정하는 평균, 분산등의 모수(parameter)를 가지고 있음
· 특정한 확률분포로부터 독립적으로 반복해 표본을 추출하는 것
· 각 관찰값들은 서로 독립적이며 동일한 분포
· 모수 : 모집단의 특성을 나타내는 값(일반적으로 알려져 있지 않음)→표본추출을 통해 모수 추정
2) 추정(통계적 추정)
· 표본으로부터 미지의 모수를 추측
가) 점추정(point estimation)
· 모수가 특정한 값일 것
· 얼마나 추정이 정확한지 판단불가
ex) 표본평균, 표본분산
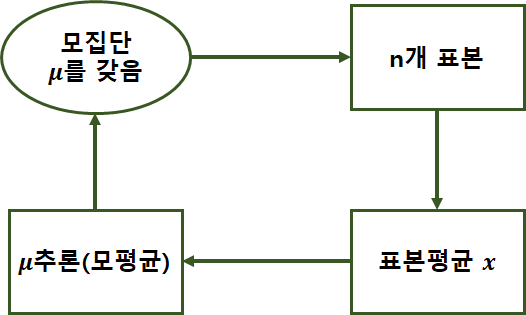
◎ 점추정량(통계량)의 조건, 표본평균, 분산
· 불편성(unbiasedness) : 모든 가능한 표본에 얻은 추정량의 기댓값은 모집단의 모수와 편의(차이)가 없음.(같다)
· 효율성(efficiency) : 추정량의 분산이 작을수록 좋음
· 일치성(consistency) : 표본의 크기가 아주 커지면, 추정량이 모수와 거의 같아진다. → 오차가 작아진다.
· 충족성(sufficient) : 추정량은 모수에 대하여 모든 정보를 제공한다.
· 10명의 학생 → 3명 표본
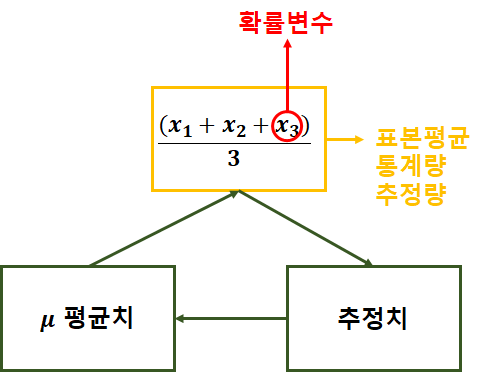
나) 구간추정(interval estimation)
· 미리 정해진 구간(99%, 95%, 90% 등)을 기준으로 모두가 참이라고 여겨질 구간을 추정하는 방법
· 모수가 특정한 구간에 있을 것이라고 선언
· 만족도 70%, 오차 2.5% → (70-2.5)% ~ (70+2.5)%
나. 가설검정
· 차의 연비 14.5L, 1인분 200g → 과연 맞는지
· 모집단에 대한 어떤 가설을 설정한 뒤에 표본 관찰을 통해 그 가설의 채택여부를 결정
· 검정하고자 하는 모집단의 모수에 대한 가설설정이 가장 기본적
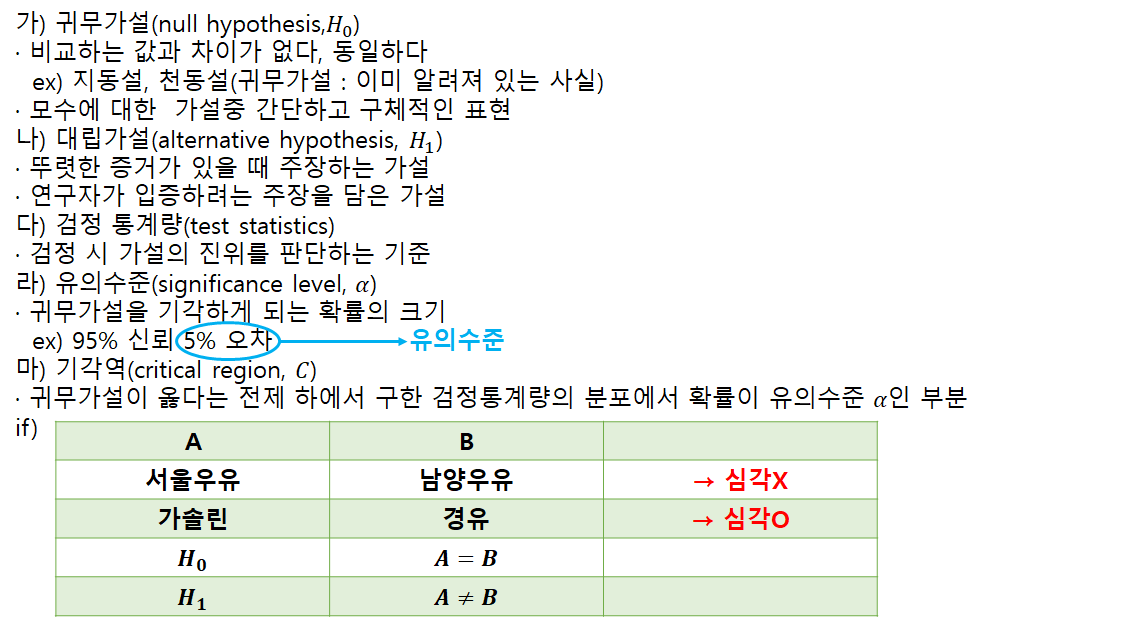
◎ 제1종오류와 제2종오류

6. 비모수 검정
가. 모수적 방법 → 정규분포를 하는 자료
· 검정하고자 하는 모집단의 분포에 대한 가정을 하고, 가장하에서 검정통계량과 검정통계량의 분포를 유도해 검정을 실시
나. 비모수적 방법 → 정규분포를 하는 자료
· 검정하고자 하는 모집단의 분포에 대한 가정을 하고, 그 가정하에서 검정통계량ㅇ과 검정통계량의 분포를 유도해 검정을 실시
· 정규분포를 하지 않는 자료 → 샘플로만 결정
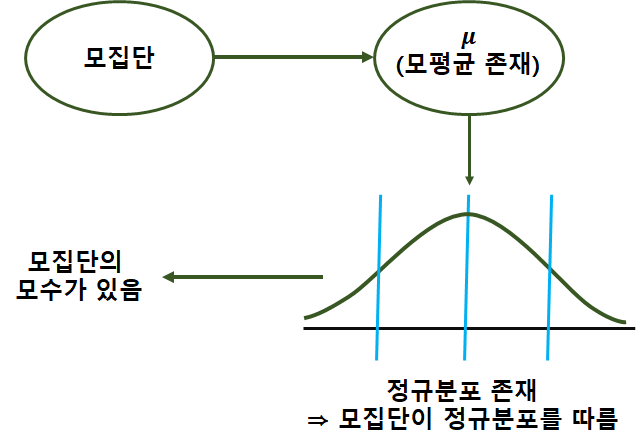
다. 모수적검정과 비모수 검정의 차이점
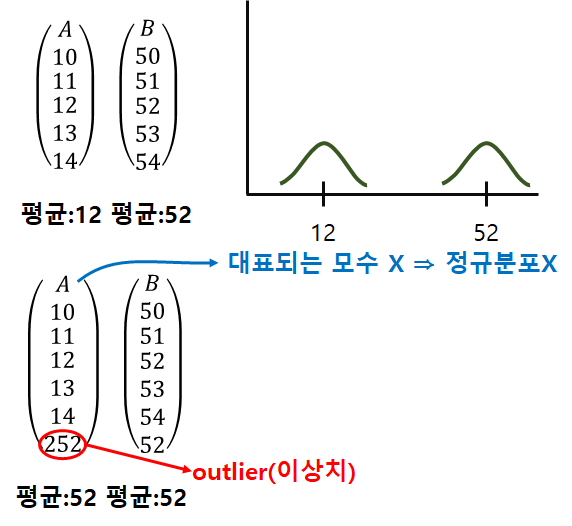
라) 비모수 검정의 예
· 쌍으로 관측된 표본에 의한 부호검정(sign test), 윌콕슨의 순위합검정(rank sum test), 윌콕슨의 부호순위합검정(Wilcoxon signed rank test), 만-위트니의 U검정, 런검정(run test), 스피어만의 순위상관계수
2절 기초 통계분석
1. 기술통계(Descriptive Statistics)
가. 기술통계의 정의
· 자료를 요약하는 기초적 통계
· 데이터 분석에 앞서 데이터의 대략적인 통계적 수치를 계산해봄으로써 데이터에 대한 대략적인 이해와 앞으로 분석에 대한 통찰력을 얻기에 유리
2. 인과관계의 이해
가. 용어
1) 종속변수(반응변수, y)
· 다른 변수의 영향을 받는 변수
2) 독립변수(설명변수, x)
· 영향을 주는 변수
3) 산점도(scatter plot)
· 좌표평면위에 점들로 표현한 그래프
> #그래픽 기능
> #산점도(scatter plot)
> #x축과 y축으로 이루어진 그래프에 두변수의 값을 점으로나타낸 그래프
> group<-c(1,1,1,2,2,2,2,2,1,1,2,1)
> age<-c(12,15,28,22,40,33,31,38,12,30,25,19)
> weight<-c(30,45,58,50,61,65,50,51,28,62,50,40)
> dat<-cbind(group,age,weight)
> dat
group age weight
[1,] 1 12 30
[2,] 1 15 45
[3,] 1 28 58
[4,] 2 22 50
[5,] 2 40 61
[6,] 2 33 65
[7,] 2 31 50
[8,] 2 38 51
[9,] 1 12 28
[10,] 1 30 62
[11,] 2 25 50
[12,] 1 19 40
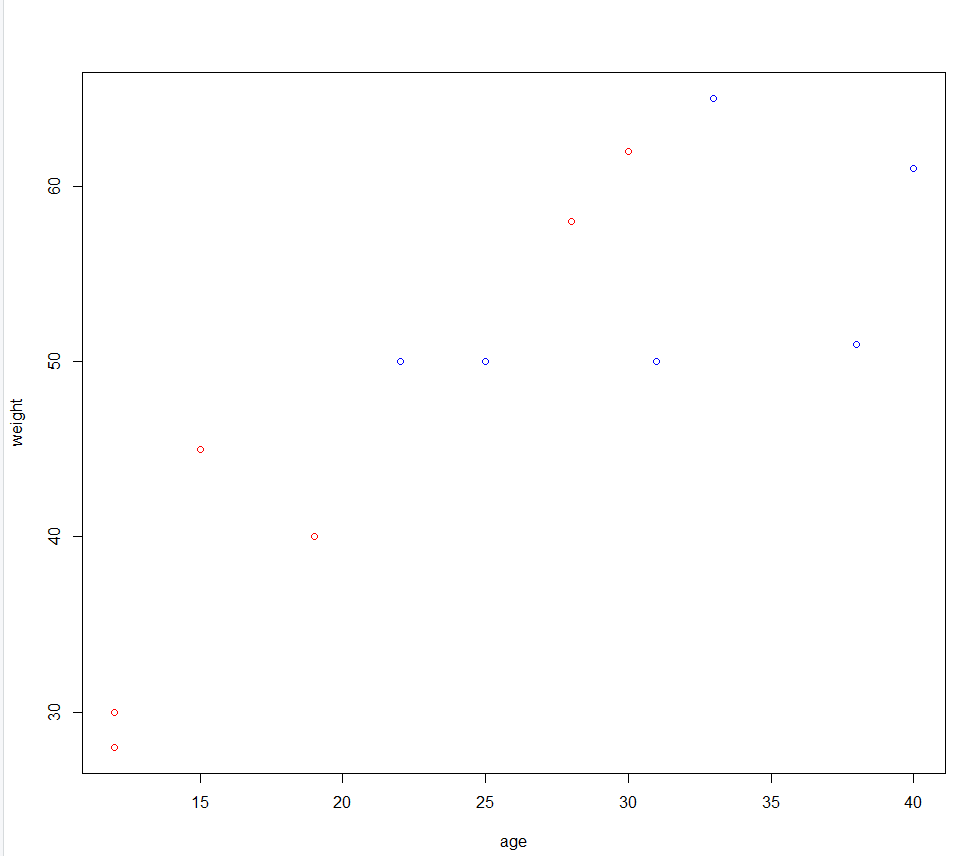
> plot(x=age,y=weight)
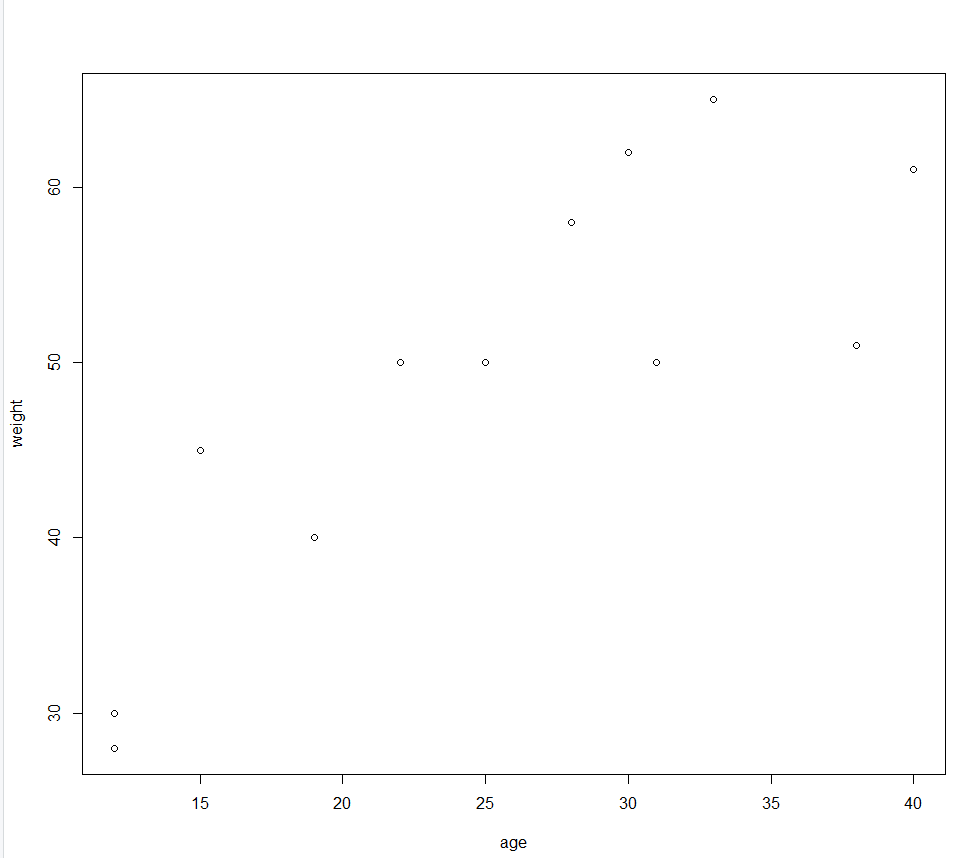
#종속변수 weight
#독립변수 age
# age에 따라서 Weight가 종속
plot(formula=weight~age,data=dat)
plot(formula=weight~age,data=dat,main="Scatter plot",xlab="age(Seoul)",ylab="weight(average)")
plot(formula=weight~age,data=dat,col=c("red","blue")[group])
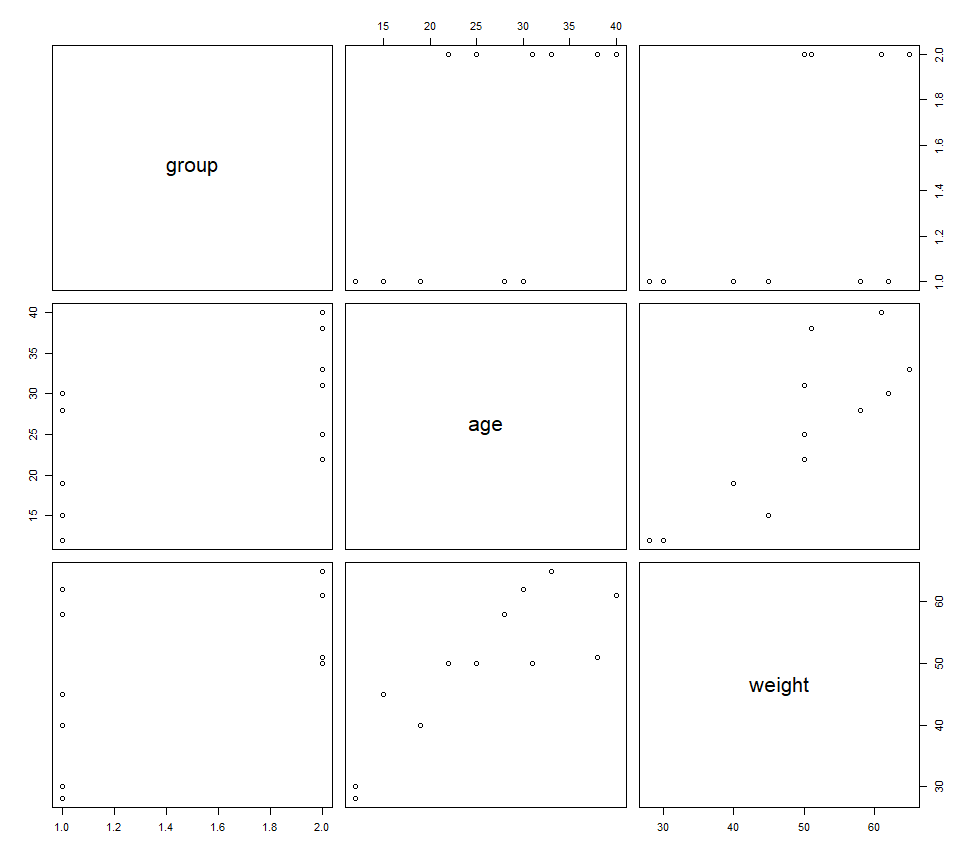
> #산점도 행렬 : 각각의 산점도를 한눈에 살펴볼 수 있도록 확장된 산점도 행렬 > #pairs() 함수 > pairs(dat)
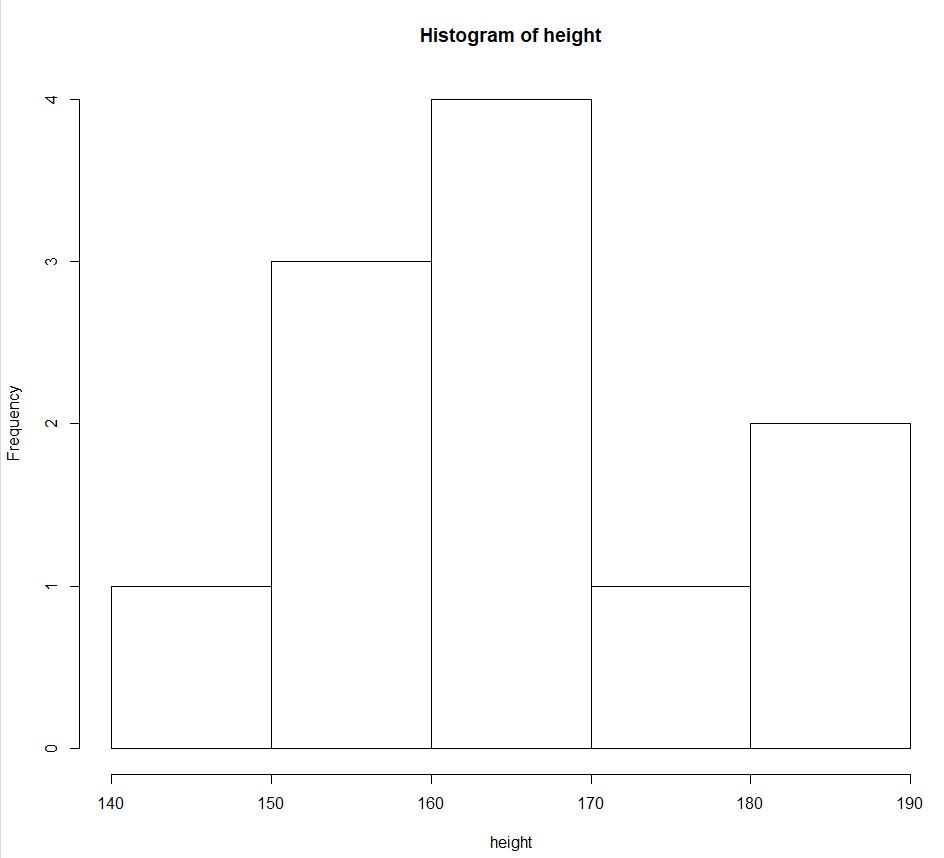
> #히스토그램 > #hist() > height<-c(182,160,165,170,163,160,181,166,159,145,175) > hist(height)
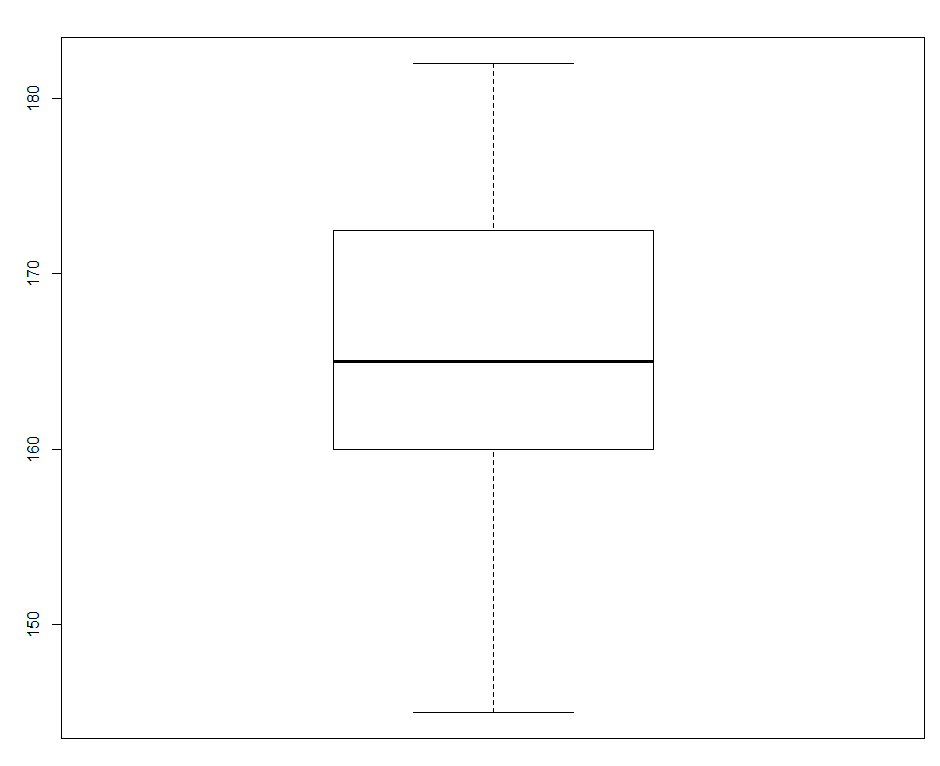
> #상자그림 > #boxplot() > boxplot(height)
나. 공분산(covariance)
· 두개 확률변수의 상관관계(상관정도) 값
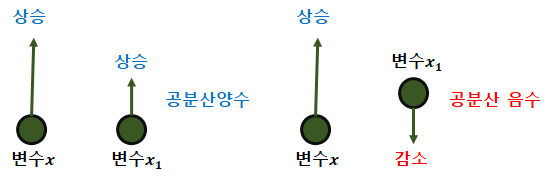
3. 상관분석(Correlation Analysis)
· 두 변수 간의 관계의 정도를 알아보기 위한 분석 방법
· 두 변수의 상관관계를 알아보기 위해 상관계수(Correlation coefficient)를 이용
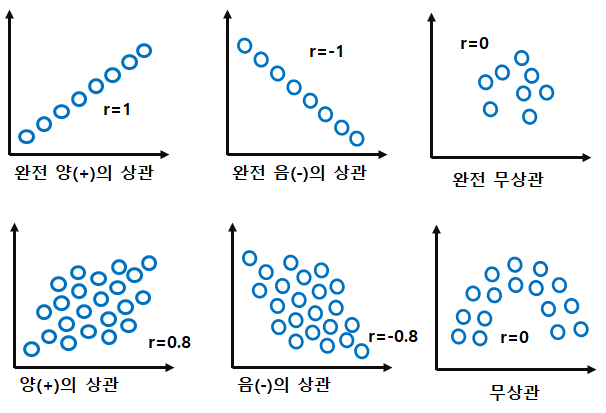
※ 상관계수
· 상관 공분산을 표준화
· 선형관계의 강도를 알수 있음. -1과 1사이의 값을 갖음.
· 0일 경우 두변수간 선형관계가 전혀X
- 0.3~0.7 : 보통 양적인 선형관계
- 0.7~1.0 : 강한 양적인 선형관계
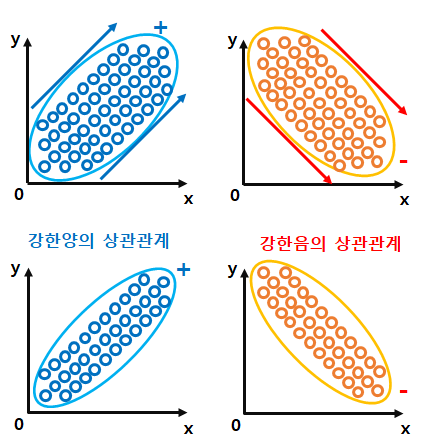
· 1(-1)에 가까울수록 강한 양(음)의 상관관계를 나타내고 상관관계가 없으면 r=0
다. 상관분석의 유형
| 구분 | 피어슨 | 스피어만 |
| 개념 | · 등간척도 이상으로 측정된 두 변수들의 상관관계 측정방식 | · 서열척도인 두변수들ㄹ의 상관관계 측정 방식 |
| 특징 | · 정규분포를 이룸, 모수이용 N | · 비모수적 검정 S |
| 상관계수 | · 피어슨(적률상관계수) | · 순위상관계수(로우) |
3절 회귀분석
1. 회귀분석 개요
가. 회귀분석의 정의
· 하나나 그 이상의 독립변수들이 종속변수에 미치는 영향을 추정(←예측←회귀식이 필요)할 수 있는 통계기법
나. 회귀분석의 변수
· 영향을 받는 변수(y) : 반응변수(response variable), 종속변수(dependent variable), 결과변수(outcom variable)
· 영향을 주는 변수(x) : 설명변수(explanatory variable), 독립변수(independent variable), 예측변수(predictor variable)
다. 선형회귀분석의 가정
1) 선형성
· 입력변수와 출력변수의 관계가 선형
2) 등분산성(오차분산일정)
· 오차의 분산이 입력변수와 무관하게 일정
3) 독립성(잔차와 독립변인 값 독립)
· 입력변수와 오차는 관련이 없음
ex) 여성몸무게 / 키 : 20명 중 10명 모수(→ 10명이 자매 or 친척 → 유전적 영향)
4) 비상관성(잔차끼라 상관X)
· 오차들끼리 상관이 없음.
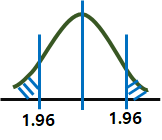
5) 정상성(정규성) (잔차가 정규분포)
· 오차의 분포가 정규분포를 따른다.
2. 단순선형회귀분석
· 하나의 종속변수와 하나의 독립변수관계를 분석


가. 회귀분석에서의 검토사항
1) 회귀계수들이 유의미한가?
· 계수의 t 통계량의 p-값이 0.05보다 작으면 해당 회귀계수가 통계적으로 유의
· 계수의 t값, p값 또는 신뢰구간 확인
· 모형이 통계적으로 유의미한가? F통계량(p값) 확인 → p-value 유의 확률 → p값 < 0.05 일정오류를 범할 확률이 0.05 미만 → 신뢰도가 높다

2) 모형이 얼마나 설명력을 갖는가?

3) 모형이 데이터를 잘 적합하고 있는가?
· 잔차를 그래프로 그리고 회귀진단
· 데이터가 전제하는 가정을 만족시키나? 선형성, 독립성, 등분산성, 비상관성, 정상성
> #단순선형회귀분석
> x<-runif(10)
> x
[1] 0.3974251 0.4147223 0.9348376 0.6880062 0.8223841 0.5236806 0.6249284 0.5232500 0.6792274 0.9669955
> y<-runif(10)
> y
[1] 0.51676954 0.65086280 0.50318965 0.38952751 0.02328749 0.33413711 0.89316259 0.53797163 0.09863120 0.20801404
> runif(10)
[1] 0.4157251 0.9143737 0.4489038 0.3868510 0.7987374 0.2985580 0.5341450 0.1913280 0.7300298 0.8253359
> set.seed(12)
> runif(10)
[1] 0.069360916 0.817775199 0.942621732 0.269381876 0.169348123 0.033895622 0.178785004 0.641665366 0.022877743 0.008324827
> #runif : random unifrom(distribution) 균등분포난수
> #runif(n,min,max)
> runif(10,0,3)
[1] 1.1780916 2.4416417 1.1287454 1.1424366 0.7947551 1.3180029 1.3728215 1.6221226 1.9970395 0.3380968
> #rnorm : 정규분포에서 난수를 생성하는 함수
> #rnorm(n,mean,sd)
> rnorm(10,0,0.2)
[1] -0.155543916 -0.258776460 -0.155913302 0.002390352 -0.030483248 -0.140692851 0.237775831 0.068102454 0.101393634 -0.058661030
> set.seed(12)
> x<-runif(10)
> y<-2+3^x+rnorm(10,0,0.2)
> df<-data.frame(x,y)
> df
x y
1 0.069360916 3.024720
2 0.817775199 4.392645
3 0.942621732 4.691077
4 0.269381876 3.323105
5 0.169348123 3.290083
6 0.033895622 2.882396
7 0.178785004 2.958256
8 0.641665366 3.867815
9 0.022877743 3.027843
10 0.008324827 2.978704
> #lm(linear model) : ln(종속변수~독립변수, 적용할데이터)
> lm(y~x, data=df)
Call:
lm(formula = y ~ x, data = df)
Coefficients:
(Intercept) x
2.873 1.811
>
> #상관계수
> #상관계수
> #Coefficients:
> #상관계수
> #Coefficients:
> # (Intercept) x
> #상관계수
> #Coefficients:
> # (Intercept) x
> # 2.873 1.811
> #상관계수
> #Coefficients:
> # (Intercept) x
> # 2.873 1.811
> # x는 회귀계수(1.811) / y절편(2.873)3. 다중선형회귀분석
· 하나의 종속변수와 둘 이상의 독립변수 간의 관계를 분석
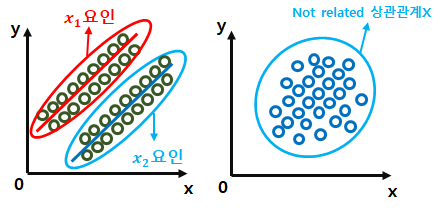
7) 다중공선성(multicollinearity)
· 독립변수의 일부가 다른 독립변수의 조합으로 표현될 수 있는 경우이다. 독립변수들이 서로 독립이 아니라 상호 상관 관계가 강한 경우에 발생한다.
· 다중공선성을 없애는 가장 기본적인 방법은 다른 독립 변수에 의존하는 변수를 없애는 것이다. 가장 의존적인 독립변수를 선택하는 방법으로는 VIF(Variance Inflation Factor)를 사용할 수 있다.
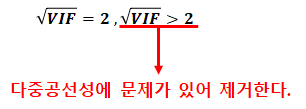
가) 분산팽창요인(VIF) : 4보다 크면 다중공선성이 존재 한다고 볼수 있고, 10보다 크면 심각한 문제가 있는 것으로 해석
나) 상태지수 : 10이상이면 문제가 있다고 보고, 30보다 크면 심각한 문제가 있다고 해석

> #다중회귀분석
> set.seed(1234)
> x1<-runif(10,0,11)
> x2<-runif(10,11,20)
> x3<-runif(10,1,30)
> y<-3+0.1^x1+2^x2-3*rnorm(10,0,0.1)
> df<-data.frame(y,x1,x2,x3)
> df
y x1 x2 x3
1 155047.461 1.2507375 17.24232 10.181761
2 61353.060 6.8452935 15.90477 9.778108
3 11952.273 6.7020221 13.54460 5.612334
4 650373.329 6.8571739 19.31090 2.159882
5 12687.334 9.4700692 13.63084 7.345187
6 380008.428 7.0434167 18.53566 24.507358
7 12215.914 0.1044533 13.57601 16.245229
8 10822.941 2.5580556 13.40139 27.525087
9 6567.525 7.3269213 12.68051 25.109006
10 8722.729 5.6567626 13.09003 2.327338
> m<-lm(y~x1+x2+x3,data=df)
> #회귀식
> #Coefficients:
> #(Intercept) x1 x2 x3
> # -801202 -3692 63818 1288
> # y = -801202 -3692x1 +63818x2 + 1288x3
> m
Call:
lm(formula = y ~ x1 + x2 + x3, data = df)
Coefficients:
(Intercept) x1 x2 x3
-1097657.4 8610.9 78675.7 -386.6
> #Coefficients:
> # Estimate Std. Error t value Pr(>|t|)
> #(Intercept) -801202 214116 -3.742 0.00960 **
> # x1 -3692 12942 -0.285 0.78500
> # x2 63818 13266 4.811 0.00297 **
> # x3 1288 4727 0.272 0.79445
> #Estimate->회귀계수
> #Pr(>|t|) -> P value 유의확률
> #Multiple R-squared: 0.8133, Adjusted R-squared: 0.72
> #F-statistic: 8.714 on 3 and 6 DF, p-value: 0.01319
> summary(m)
Call:
lm(formula = y ~ x1 + x2 + x3, data = df)
Residuals:
Min 1Q Median 3Q Max
-147472 -38536 8571 46048 170521
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1097657.4 255569.3 -4.295 0.00512 **
x1 8610.9 12547.8 0.686 0.51818
x2 78675.7 15187.6 5.180 0.00205 **
x3 -386.6 3974.6 -0.097 0.92567
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 110700 on 6 degrees of freedom
Multiple R-squared: 0.8266, Adjusted R-squared: 0.7399
F-statistic: 9.533 on 3 and 6 DF, p-value: 0.01064
> # R-squared 결정계수 81.33%의 신뢰성
> # p-value: 0.01319 ->0.05 밑의 값 신뢰성 크다
> # MASS 패키지에는 Diet 를 적용한 닭에 대한 데이터가 들어 있음.
> #install.packages("MASS")
> library(MASS)
> head(ChickWeight)
weight Time Chick Diet
1 42 0 1 1
2 51 2 1 1
3 59 4 1 1
4 64 6 1 1
5 76 8 1 1
6 93 10 1 1
> chick<-ChickWeight[ChickWeight$Diet==1,]
> chick
weight Time Chick Diet
1 42 0 1 1
2 51 2 1 1
3 59 4 1 1
4 64 6 1 1
5 76 8 1 1
6 93 10 1 1
7 106 12 1 1
8 125 14 1 1
.......
214 73 10 20 1
215 77 12 20 1
216 89 14 20 1
217 98 16 20 1
218 107 18 20 1
219 115 20 20 1
220 117 21 20 1
> chick<-ChickWeight[ChickWeight$Chick==1,]
> chick
weight Time Chick Diet
1 42 0 1 1
2 51 2 1 1
3 59 4 1 1
4 64 6 1 1
5 76 8 1 1
6 93 10 1 1
7 106 12 1 1
8 125 14 1 1
9 149 16 1 1
10 171 18 1 1
11 199 20 1 1
12 205 21 1 1
> # 시간의 경과에 따른 닭들의 무게를 단순회귀 분석
> lm(weight~Time,chick)
Call:
lm(formula = weight ~ Time, data = chick)
Coefficients:
(Intercept) Time
24.465 7.988
> #회귀식 weight = 24.465+7.988*Time
> m1<-lm(weight~Time,chick)
> summary(m1)
Call:
lm(formula = weight ~ Time, data = chick)
Residuals:
Min 1Q Median 3Q Max
-14.3202 -11.3081 -0.3444 11.1162 17.5346
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 24.4654 6.7279 3.636 0.00456 **
Time 7.9879 0.5236 15.255 2.97e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 12.29 on 10 degrees of freedom
Multiple R-squared: 0.9588, Adjusted R-squared: 0.9547
F-statistic: 232.7 on 1 and 10 DF, p-value: 2.974e-08
> #회귀진단
> data(cars)
> head(cars)
speed dist
1 4 2
2 4 10
3 7 4
4 7 22
5 8 16
6 9 10
> #dist 제동거리
> mm<-lm(dist~speed,cars)
> mm
Call:
lm(formula = dist ~ speed, data = cars)
Coefficients:
(Intercept) speed
-17.579 3.932
> summary(mm)
Call:
lm(formula = dist ~ speed, data = cars)
Residuals:
Min 1Q Median 3Q Max
-29.069 -9.525 -2.272 9.215 43.201
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -17.5791 6.7584 -2.601 0.0123 *
speed 3.9324 0.4155 9.464 1.49e-12 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 15.38 on 48 degrees of freedom
Multiple R-squared: 0.6511, Adjusted R-squared: 0.6438
F-statistic: 89.57 on 1 and 48 DF, p-value: 1.49e-12
plot(mm)* plot(mm)
① Residuals 잔차(plat해야됨) : 제곱계산 OLS(최소제곱승)
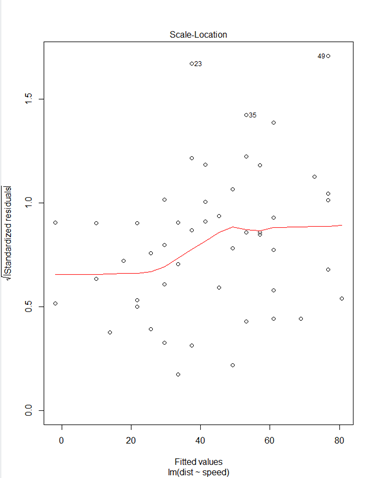
② 표준잔차(등분산성) -> 기울기가 0이여야됨
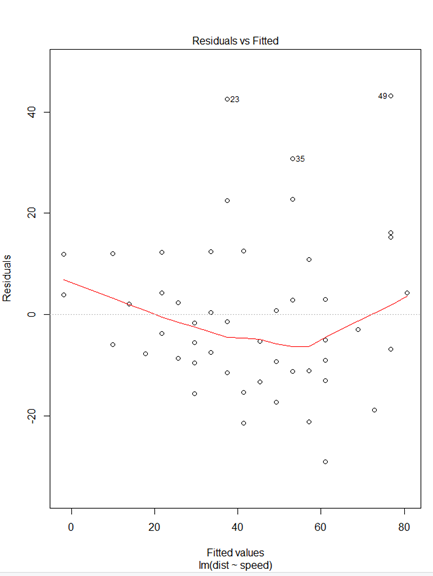
③ 정규분포 선상에 있어야 정규분포를 잘따른다.
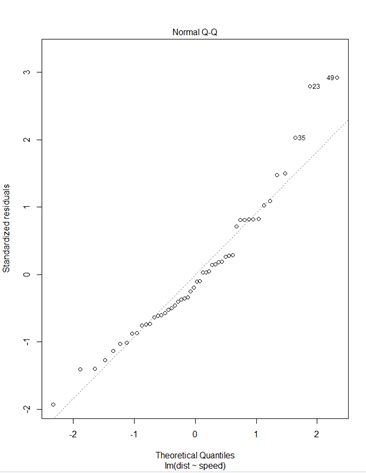
④ 이상치 / 큰지렛점 / 영향(이상)관측치
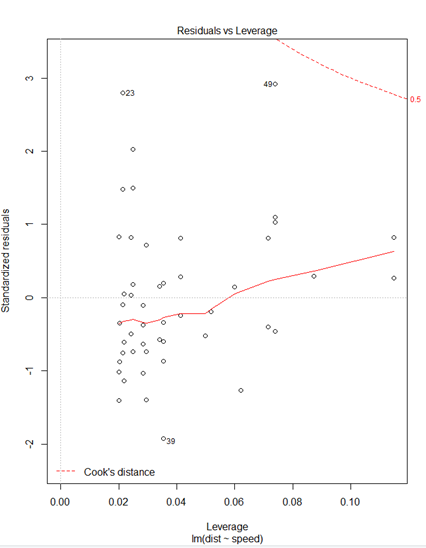
> #큰지레점계산
> nrow(cars)
[1] 50
> (2/50)*3
[1] 0.12
> women
height weight
1 58 115
2 59 117
3 60 120
4 61 123
5 62 126
6 63 129
7 64 132
8 65 135
9 66 139
10 67 142
11 68 146
12 69 150
13 70 154
14 71 159
15 72 164
> fit<-lm(weight~height,data=women)
> fit
Call:
lm(formula = weight ~ height, data = women)
Coefficients:
(Intercept) height
-87.52 3.45
> #회귀식 weight =3.45height -87.52
> plot(fit)
> plot(weight~height,data=women)
* plot(fit)
① Residuals 잔차(plat해야됨) : 제곱계산 OLS(최소제곱승)
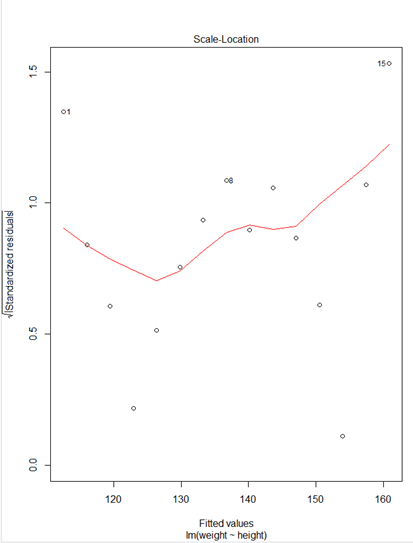
② 표준잔차(등분산성) -> 기울기가 0이여야됨
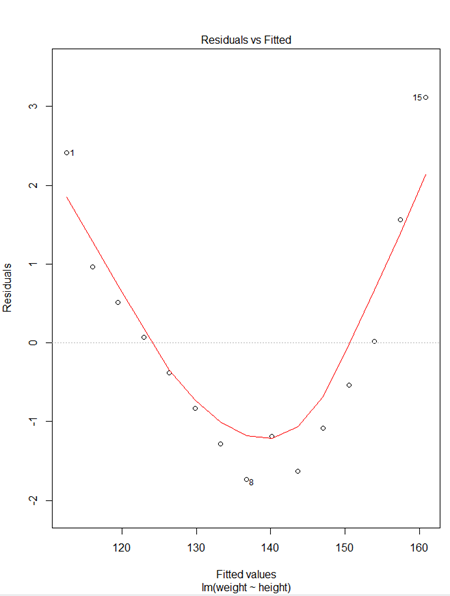
③ 정규분포 선상에 있어야 정규분포를 잘따른다.
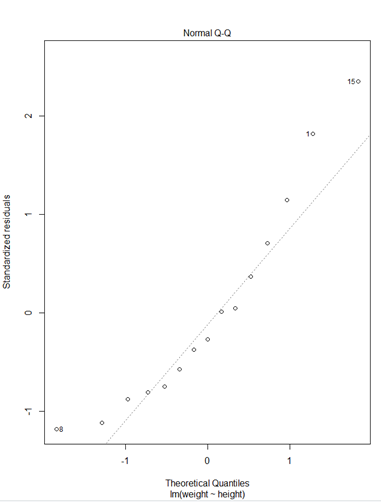
④ 이상치 / 큰지렛점 / 영향(이상)관측치
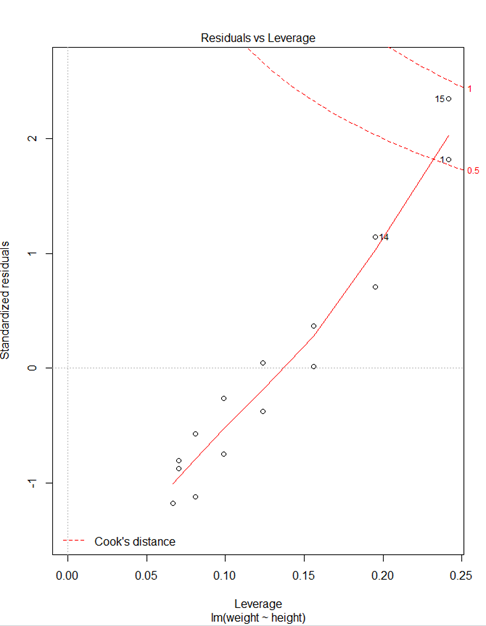
* plot(weight~height,data=women)
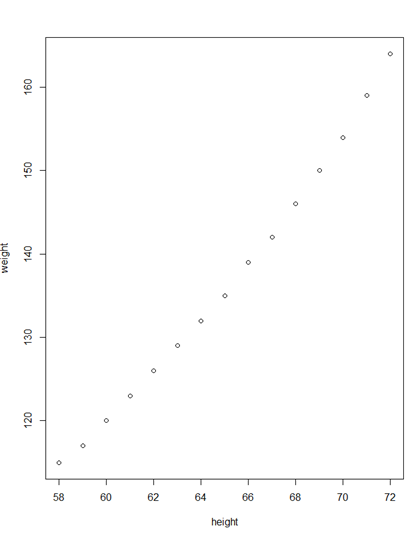
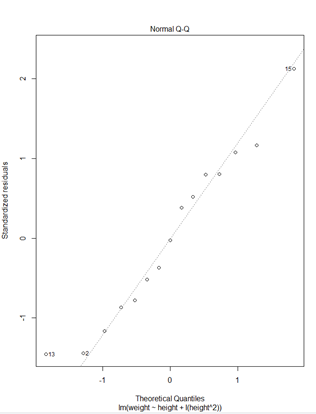
> ### 다항회귀모형#### > fit2<-lm(weight~height+I(height^2),data=women) > plot(fit2)
* plot(fit2)
① Residuals 잔차(plat해야됨) : 제곱계산 OLS(최소제곱승)
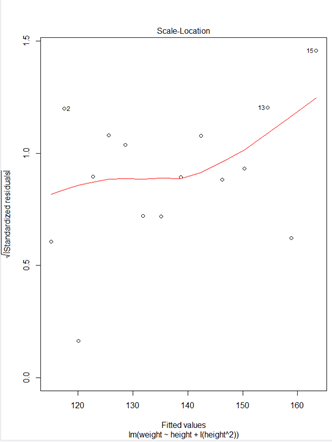
② 표준잔차(등분산성) -> 기울기가 0이여야됨
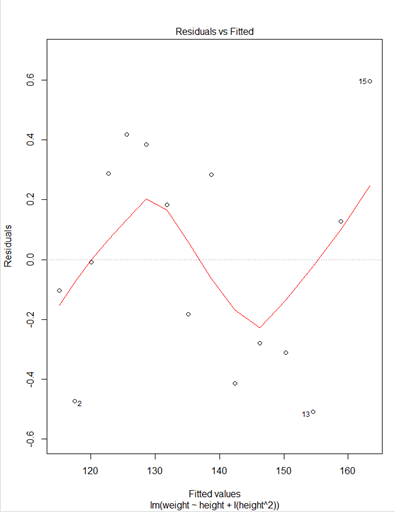
③ 정규분포 선상에 있어야 정규분포를 잘따른다.
④ 이상치 / 큰지렛점 / 영향(이상)관측치
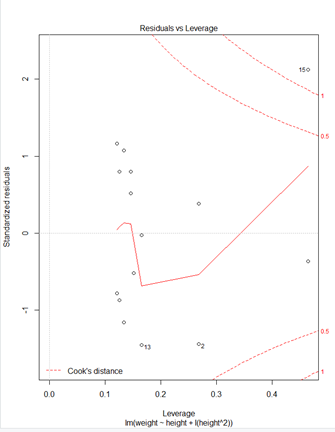
> ##다중회귀모형##
> nrow(state.x77)
[1] 50
> state.x77
Population Income Illiteracy Life Exp Murder HS Grad Frost Area
Alabama 3615 3624 2.1 69.05 15.1 41.3 20 50708
Alaska 365 6315 1.5 69.31 11.3 66.7 152 566432
Arizona 2212 4530 1.8 70.55 7.8 58.1 15 113417
Arkansas 2110 3378 1.9 70.66 10.1 39.9 65 51945
California 21198 5114 1.1 71.71 10.3 62.6 20 156361
Colorado 2541 4884 0.7 72.06 6.8 63.9 166 103766
Connecticut 3100 5348 1.1 72.48 3.1 56.0 139 4862
Delaware 579 4809 0.9 70.06 6.2 54.6 103 1982
Florida 8277 4815 1.3 70.66 10.7 52.6 11 54090
Georgia 4931 4091 2.0 68.54 13.9 40.6 60 58073
Hawaii 868 4963 1.9 73.60 6.2 61.9 0 6425
Idaho 813 4119 0.6 71.87 5.3 59.5 126 82677
Illinois 11197 5107 0.9 70.14 10.3 52.6 127 55748
Indiana 5313 4458 0.7 70.88 7.1 52.9 122 36097
Iowa 2861 4628 0.5 72.56 2.3 59.0 140 55941
Kansas 2280 4669 0.6 72.58 4.5 59.9 114 81787
Kentucky 3387 3712 1.6 70.10 10.6 38.5 95 39650
Louisiana 3806 3545 2.8 68.76 13.2 42.2 12 44930
Maine 1058 3694 0.7 70.39 2.7 54.7 161 30920
Maryland 4122 5299 0.9 70.22 8.5 52.3 101 9891
Massachusetts 5814 4755 1.1 71.83 3.3 58.5 103 7826
Michigan 9111 4751 0.9 70.63 11.1 52.8 125 56817
Minnesota 3921 4675 0.6 72.96 2.3 57.6 160 79289
Mississippi 2341 3098 2.4 68.09 12.5 41.0 50 47296
Missouri 4767 4254 0.8 70.69 9.3 48.8 108 68995
Montana 746 4347 0.6 70.56 5.0 59.2 155 145587
Nebraska 1544 4508 0.6 72.60 2.9 59.3 139 76483
Nevada 590 5149 0.5 69.03 11.5 65.2 188 109889
New Hampshire 812 4281 0.7 71.23 3.3 57.6 174 9027
New Jersey 7333 5237 1.1 70.93 5.2 52.5 115 7521
New Mexico 1144 3601 2.2 70.32 9.7 55.2 120 121412
New York 18076 4903 1.4 70.55 10.9 52.7 82 47831
North Carolina 5441 3875 1.8 69.21 11.1 38.5 80 48798
North Dakota 637 5087 0.8 72.78 1.4 50.3 186 69273
Ohio 10735 4561 0.8 70.82 7.4 53.2 124 40975
Oklahoma 2715 3983 1.1 71.42 6.4 51.6 82 68782
Oregon 2284 4660 0.6 72.13 4.2 60.0 44 96184
Pennsylvania 11860 4449 1.0 70.43 6.1 50.2 126 44966
Rhode Island 931 4558 1.3 71.90 2.4 46.4 127 1049
South Carolina 2816 3635 2.3 67.96 11.6 37.8 65 30225
South Dakota 681 4167 0.5 72.08 1.7 53.3 172 75955
Tennessee 4173 3821 1.7 70.11 11.0 41.8 70 41328
Texas 12237 4188 2.2 70.90 12.2 47.4 35 262134
Utah 1203 4022 0.6 72.90 4.5 67.3 137 82096
Vermont 472 3907 0.6 71.64 5.5 57.1 168 9267
Virginia 4981 4701 1.4 70.08 9.5 47.8 85 39780
Washington 3559 4864 0.6 71.72 4.3 63.5 32 66570
West Virginia 1799 3617 1.4 69.48 6.7 41.6 100 24070
Wisconsin 4589 4468 0.7 72.48 3.0 54.5 149 54464
Wyoming 376 4566 0.6 70.29 6.9 62.9 173 97203
> states<-as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])
> states
Murder Population Illiteracy Income Frost
Alabama 15.1 3615 2.1 3624 20
Alaska 11.3 365 1.5 6315 152
Arizona 7.8 2212 1.8 4530 15
Arkansas 10.1 2110 1.9 3378 65
California 10.3 21198 1.1 5114 20
Colorado 6.8 2541 0.7 4884 166
Connecticut 3.1 3100 1.1 5348 139
Delaware 6.2 579 0.9 4809 103
Florida 10.7 8277 1.3 4815 11
Georgia 13.9 4931 2.0 4091 60
Hawaii 6.2 868 1.9 4963 0
Idaho 5.3 813 0.6 4119 126
Illinois 10.3 11197 0.9 5107 127
Indiana 7.1 5313 0.7 4458 122
Iowa 2.3 2861 0.5 4628 140
Kansas 4.5 2280 0.6 4669 114
Kentucky 10.6 3387 1.6 3712 95
Louisiana 13.2 3806 2.8 3545 12
Maine 2.7 1058 0.7 3694 161
Maryland 8.5 4122 0.9 5299 101
Massachusetts 3.3 5814 1.1 4755 103
Michigan 11.1 9111 0.9 4751 125
Minnesota 2.3 3921 0.6 4675 160
Mississippi 12.5 2341 2.4 3098 50
Missouri 9.3 4767 0.8 4254 108
Montana 5.0 746 0.6 4347 155
Nebraska 2.9 1544 0.6 4508 139
Nevada 11.5 590 0.5 5149 188
New Hampshire 3.3 812 0.7 4281 174
New Jersey 5.2 7333 1.1 5237 115
New Mexico 9.7 1144 2.2 3601 120
New York 10.9 18076 1.4 4903 82
North Carolina 11.1 5441 1.8 3875 80
North Dakota 1.4 637 0.8 5087 186
Ohio 7.4 10735 0.8 4561 124
Oklahoma 6.4 2715 1.1 3983 82
Oregon 4.2 2284 0.6 4660 44
Pennsylvania 6.1 11860 1.0 4449 126
Rhode Island 2.4 931 1.3 4558 127
South Carolina 11.6 2816 2.3 3635 65
South Dakota 1.7 681 0.5 4167 172
Tennessee 11.0 4173 1.7 3821 70
Texas 12.2 12237 2.2 4188 35
Utah 4.5 1203 0.6 4022 137
Vermont 5.5 472 0.6 3907 168
Virginia 9.5 4981 1.4 4701 85
Washington 4.3 3559 0.6 4864 32
West Virginia 6.7 1799 1.4 3617 100
Wisconsin 3.0 4589 0.7 4468 149
Wyoming 6.9 376 0.6 4566 173
> fit <- lm(Murder~Population+Illiteracy+Income+Frost,data=states)
> summary(fit)
Call:
lm(formula = Murder ~ Population + Illiteracy + Income + Frost,
data = states)
Residuals:
Min 1Q Median 3Q Max
-4.7960 -1.6495 -0.0811 1.4815 7.6210
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.235e+00 3.866e+00 0.319 0.7510
Population 2.237e-04 9.052e-05 2.471 0.0173 *
Illiteracy 4.143e+00 8.744e-01 4.738 2.19e-05 ***
Income 6.442e-05 6.837e-04 0.094 0.9253
Frost 5.813e-04 1.005e-02 0.058 0.9541
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.535 on 45 degrees of freedom
Multiple R-squared: 0.567, Adjusted R-squared: 0.5285
F-statistic: 14.73 on 4 and 45 DF, p-value: 9.133e-08
> #install.packages("car",dependencies = TRUE)
> library(car)
> vif(fit)
Population Illiteracy Income Frost
1.245282 2.165848 1.345822 2.082547
> #Population Illiteracy Income Frost
> #1.245282 2.165848 1.345822 2.082547
> #vif 값이 4이상이 없음
> sqrt(vif(fit))
Population Illiteracy Income Frost
1.115922 1.471682 1.160096 1.443103
> plot(fit)① Residuals 잔차(plat해야됨) : 제곱계산 OLS(최소제곱승)
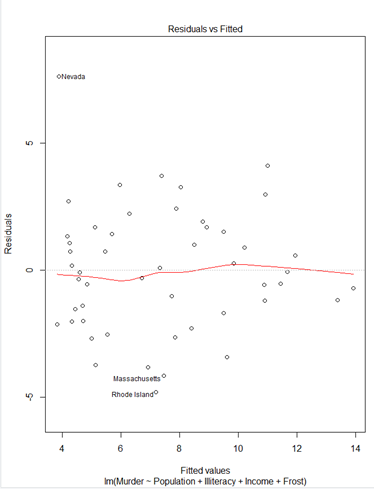
② 표준잔차(등분산성) -> 기울기가 0이여야됨
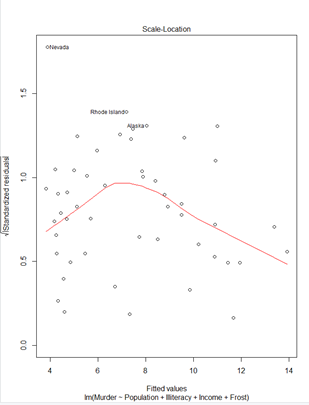
③ 정규분포 선상에 있어야 정규분포를 잘따른다.
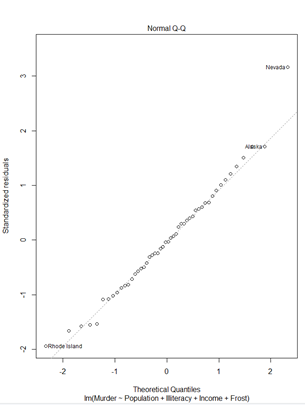
④ 이상치 / 큰지렛점 / 영향(이상)관측치
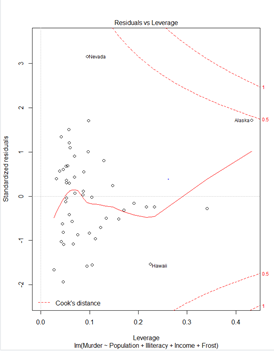
6. 최적회귀방정식
가. 최적회귀방정식의 선택
1) 설명변수 선택
· y에 영향을 미칠 수 있는 모ㅗ든 설명변수 x들을 y의 값을 예측하는데 참여
· 데이터에 설명변수 x들의 수가 맣아지면 관리하는데 많은 노력이 요구되므로, 가능한 범위내에서 적은수의 설명변수를 포함
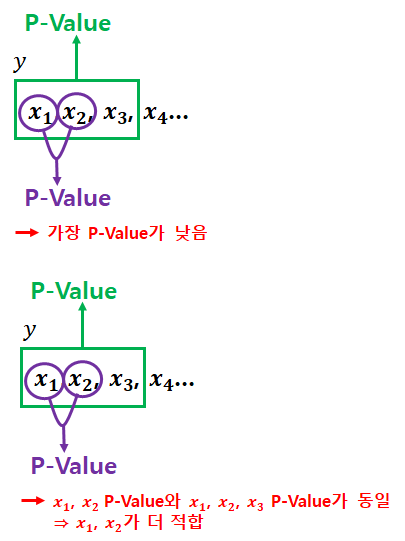
2) 모형선택(exploratory analysis) : 분석데이터에 가장 잘 맞는 모형을 찾아내는 방법
· 모든 가능한 조합의 회귀분석(All possible regression) : 모든 가능한 독립변수들의 조합에 대한 회귀모형을 생성한 뒤 가장 적합한 회귀모형을 선택 → AIC(더 많이 사용) / BIC
3) 단계적 변수 선택(Stepwise Variable Selection)
· 전진선택법(forward selection) : 절편만 있는 상수모형으로부터 시작해 중요하다고 생각되는 설명변수부터 차례로 모형에 추가
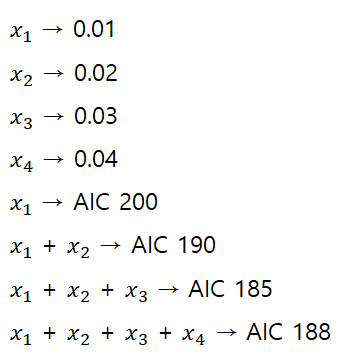
· 후진제거법(backward elimination, 후위선택법) : 독립변수 후보 모두를 포함한 모형에서 출발해 가장 적은 영향을 주는 변수부터 하나씩 제거하면서 더 이상 제거할 변수가 없을 때의 모형을 선택

· 단계선택법(stepwise method) : 추가또는 제거
- 모든 변수가 포함된 모델에서 출발하여 기준통계치에 가장 도움이 되지 않는 변수를 삭제하거나, 모델에서 빠져있는 변수 중에서 기준통계치를 가장 개선시키는 변수를 추가한다. 그리고 이러한 변수의 추가 또는 삭제를 반복한다. 반대로 절편만 포함된 모델에서 출발해 변수의 추가 삭제를 반복할 수도 있다.

· step(lm(종속변수~설명변수,데이터셋),scope=list(lower=~,upper=~설명변수),direction="변수선택방법") 함수로 쉽게 선택가능
> #단계별 선택방법
> # backward stepwise regression(backward selection(elimination))
> #library(mlbench)
> #data(BostonHousing)
> states
Murder Population Illiteracy Income Frost
Alabama 15.1 3615 2.1 3624 20
Alaska 11.3 365 1.5 6315 152
Arizona 7.8 2212 1.8 4530 15
Arkansas 10.1 2110 1.9 3378 65
California 10.3 21198 1.1 5114 20
Colorado 6.8 2541 0.7 4884 166
Connecticut 3.1 3100 1.1 5348 139
Delaware 6.2 579 0.9 4809 103
Florida 10.7 8277 1.3 4815 11
Georgia 13.9 4931 2.0 4091 60
Hawaii 6.2 868 1.9 4963 0
Idaho 5.3 813 0.6 4119 126
Illinois 10.3 11197 0.9 5107 127
Indiana 7.1 5313 0.7 4458 122
Iowa 2.3 2861 0.5 4628 140
Kansas 4.5 2280 0.6 4669 114
Kentucky 10.6 3387 1.6 3712 95
Louisiana 13.2 3806 2.8 3545 12
Maine 2.7 1058 0.7 3694 161
Maryland 8.5 4122 0.9 5299 101
Massachusetts 3.3 5814 1.1 4755 103
Michigan 11.1 9111 0.9 4751 125
Minnesota 2.3 3921 0.6 4675 160
Mississippi 12.5 2341 2.4 3098 50
Missouri 9.3 4767 0.8 4254 108
Montana 5.0 746 0.6 4347 155
Nebraska 2.9 1544 0.6 4508 139
Nevada 11.5 590 0.5 5149 188
New Hampshire 3.3 812 0.7 4281 174
New Jersey 5.2 7333 1.1 5237 115
New Mexico 9.7 1144 2.2 3601 120
New York 10.9 18076 1.4 4903 82
North Carolina 11.1 5441 1.8 3875 80
North Dakota 1.4 637 0.8 5087 186
Ohio 7.4 10735 0.8 4561 124
Oklahoma 6.4 2715 1.1 3983 82
Oregon 4.2 2284 0.6 4660 44
Pennsylvania 6.1 11860 1.0 4449 126
Rhode Island 2.4 931 1.3 4558 127
South Carolina 11.6 2816 2.3 3635 65
South Dakota 1.7 681 0.5 4167 172
Tennessee 11.0 4173 1.7 3821 70
Texas 12.2 12237 2.2 4188 35
Utah 4.5 1203 0.6 4022 137
Vermont 5.5 472 0.6 3907 168
Virginia 9.5 4981 1.4 4701 85
Washington 4.3 3559 0.6 4864 32
West Virginia 6.7 1799 1.4 3617 100
Wisconsin 3.0 4589 0.7 4468 149
Wyoming 6.9 376 0.6 4566 173
> full.model<-lm(Murder~.,data=states)
> summary(full.model)
Call:
lm(formula = Murder ~ ., data = states)
Residuals:
Min 1Q Median 3Q Max
-4.7960 -1.6495 -0.0811 1.4815 7.6210
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.235e+00 3.866e+00 0.319 0.7510
Population 2.237e-04 9.052e-05 2.471 0.0173 *
Illiteracy 4.143e+00 8.744e-01 4.738 2.19e-05 ***
Income 6.442e-05 6.837e-04 0.094 0.9253
Frost 5.813e-04 1.005e-02 0.058 0.9541
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.535 on 45 degrees of freedom
Multiple R-squared: 0.567, Adjusted R-squared: 0.5285
F-statistic: 14.73 on 4 and 45 DF, p-value: 9.133e-08
> full.model1<-lm(Murder~Population+Illiteracy,data=states)
> summary(full.model)
Call:
lm(formula = Murder ~ ., data = states)
Residuals:
Min 1Q Median 3Q Max
-4.7960 -1.6495 -0.0811 1.4815 7.6210
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.235e+00 3.866e+00 0.319 0.7510
Population 2.237e-04 9.052e-05 2.471 0.0173 *
Illiteracy 4.143e+00 8.744e-01 4.738 2.19e-05 ***
Income 6.442e-05 6.837e-04 0.094 0.9253
Frost 5.813e-04 1.005e-02 0.058 0.9541
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.535 on 45 degrees of freedom
Multiple R-squared: 0.567, Adjusted R-squared: 0.5285
F-statistic: 14.73 on 4 and 45 DF, p-value: 9.133e-08
> full.model2<-lm(Murder~Population+Illiteracy+Income,data=states)
> summary(full.model)
Call:
lm(formula = Murder ~ ., data = states)
Residuals:
Min 1Q Median 3Q Max
-4.7960 -1.6495 -0.0811 1.4815 7.6210
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.235e+00 3.866e+00 0.319 0.7510
Population 2.237e-04 9.052e-05 2.471 0.0173 *
Illiteracy 4.143e+00 8.744e-01 4.738 2.19e-05 ***
Income 6.442e-05 6.837e-04 0.094 0.9253
Frost 5.813e-04 1.005e-02 0.058 0.9541
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.535 on 45 degrees of freedom
Multiple R-squared: 0.567, Adjusted R-squared: 0.5285
F-statistic: 14.73 on 4 and 45 DF, p-value: 9.133e-08
> # AIC(Akaike's an Information Criterion)
> AIC(full.model,full.model1,full.model2)
df AIC
full.model 6 241.6429
full.model1 4 237.6565
full.model2 5 239.6467
> reduced.model<-step(full.model,direction ="backward")
Start: AIC=97.75
Murder ~ Population + Illiteracy + Income + Frost
Df Sum of Sq RSS AIC
- Frost 1 0.021 289.19 95.753
- Income 1 0.057 289.22 95.759
<none> 289.17 97.749
- Population 1 39.238 328.41 102.111
- Illiteracy 1 144.264 433.43 115.986
Step: AIC=95.75
Murder ~ Population + Illiteracy + Income
Df Sum of Sq RSS AIC
- Income 1 0.057 289.25 93.763
<none> 289.19 95.753
- Population 1 43.658 332.85 100.783
- Illiteracy 1 236.196 525.38 123.605
Step: AIC=93.76
Murder ~ Population + Illiteracy
Df Sum of Sq RSS AIC
<none> 289.25 93.763
- Population 1 48.517 337.76 99.516
- Illiteracy 1 299.646 588.89 127.311
> summary(reduced.model)
Call:
lm(formula = Murder ~ Population + Illiteracy, data = states)
Residuals:
Min 1Q Median 3Q Max
-4.7652 -1.6561 -0.0898 1.4570 7.6758
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.652e+00 8.101e-01 2.039 0.04713 *
Population 2.242e-04 7.984e-05 2.808 0.00724 **
Illiteracy 4.081e+00 5.848e-01 6.978 8.83e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.481 on 47 degrees of freedom
Multiple R-squared: 0.5668, Adjusted R-squared: 0.5484
F-statistic: 30.75 on 2 and 47 DF, p-value: 2.893e-09
> #Forward stepwise regressiion
> min.model<-lm(Murder~1,data=states) #1 : y=b+ax 에서b 상수값
> min.model
Call:
lm(formula = Murder ~ 1, data = states)
Coefficients:
(Intercept)
7.378
> forward.model<-step(min.model,scope = (Murder~Population + Illiteracy + Income + Frost),direction = "forward")
Start: AIC=131.59
Murder ~ 1
Df Sum of Sq RSS AIC
+ Illiteracy 1 329.98 337.76 99.516
+ Frost 1 193.91 473.84 116.442
+ Population 1 78.85 588.89 127.311
+ Income 1 35.35 632.40 130.875
<none> 667.75 131.594
Step: AIC=99.52
Murder ~ Illiteracy
Df Sum of Sq RSS AIC
+ Population 1 48.517 289.25 93.763
<none> 337.76 99.516
+ Frost 1 5.387 332.38 100.712
+ Income 1 4.916 332.85 100.783
Step: AIC=93.76
Murder ~ Illiteracy + Population
Df Sum of Sq RSS AIC
<none> 289.25 93.763
+ Income 1 0.057022 289.19 95.753
+ Frost 1 0.021447 289.22 95.759
> summary(forward.model)
Call:
lm(formula = Murder ~ Illiteracy + Population, data = states)
Residuals:
Min 1Q Median 3Q Max
-4.7652 -1.6561 -0.0898 1.4570 7.6758
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.652e+00 8.101e-01 2.039 0.04713 *
Illiteracy 4.081e+00 5.848e-01 6.978 8.83e-09 ***
Population 2.242e-04 7.984e-05 2.808 0.00724 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.481 on 47 degrees of freedom
Multiple R-squared: 0.5668, Adjusted R-squared: 0.5484
F-statistic: 30.75 on 2 and 47 DF, p-value: 2.893e-09
> # Stepwise regression
> both.model<-step(full.model,direction="both")
Start: AIC=97.75
Murder ~ Population + Illiteracy + Income + Frost
Df Sum of Sq RSS AIC
- Frost 1 0.021 289.19 95.753
- Income 1 0.057 289.22 95.759
<none> 289.17 97.749
- Population 1 39.238 328.41 102.111
- Illiteracy 1 144.264 433.43 115.986
Step: AIC=95.75
Murder ~ Population + Illiteracy + Income
Df Sum of Sq RSS AIC
- Income 1 0.057 289.25 93.763
<none> 289.19 95.753
+ Frost 1 0.021 289.17 97.749
- Population 1 43.658 332.85 100.783
- Illiteracy 1 236.196 525.38 123.605
Step: AIC=93.76
Murder ~ Population + Illiteracy
Df Sum of Sq RSS AIC
<none> 289.25 93.763
+ Income 1 0.057 289.19 95.753
+ Frost 1 0.021 289.22 95.759
- Population 1 48.517 337.76 99.516
- Illiteracy 1 299.646 588.89 127.311
> summary(both.model)
Call:
lm(formula = Murder ~ Population + Illiteracy, data = states)
Residuals:
Min 1Q Median 3Q Max
-4.7652 -1.6561 -0.0898 1.4570 7.6758
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.652e+00 8.101e-01 2.039 0.04713 *
Population 2.242e-04 7.984e-05 2.808 0.00724 **
Illiteracy 4.081e+00 5.848e-01 6.978 8.83e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.481 on 47 degrees of freedom
Multiple R-squared: 0.5668, Adjusted R-squared: 0.5484
F-statistic: 30.75 on 2 and 47 DF, p-value: 2.893e-09
> #all subset regression
> library(leaps)
> leap<-regsubsets(Murder~Population + Illiteracy + Income + Frost,data = states,nbest=2)
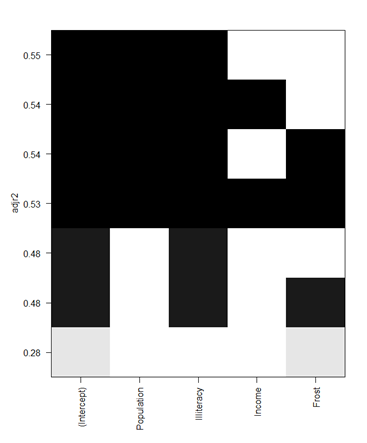
> plot(leap,scale="adjr2")
> #y축 R^2(결정계수)
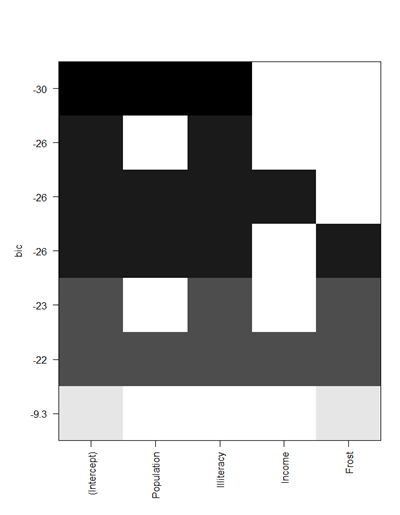
> plot(leap,scale="bic")* plot(leap,scale="adjr2")
* plot(leap,scale="bic")
4절 시계열 분석
1. 시계열 자료
가. 개요
· 시간의 흐름에 따라 관찰된 값(ex) 주가)
나. 시계열 자료의 종류
1) 비정상성 시계열 자료
· 시계열 분석을 실시할 때 다루기 어려운 자료
2) 정상성 시계열 자료
· 비정상 시계열을 정상 시계열로 만들어 분석
* 비정상 → 정상 : 변환, 차분
2. 정상성
가. 평균이 일정
· 모든 시점에 대해 일정한 평균을 가짐
· 평균이 일정하지 않은 시계열은 차분(difference)을 통해 정상화
· (t1 - t0) : 시간차 → 현시점자료 - 전시점자료
나. 분산이 일정(시점과는 상관없이 분산값이 항상 일정)
· 분산도 시점에 의존하지 않고 일정(시점과 분산의 독립)
· 분산이 일정하지 않을 경우 변환(Transformation)을 통해 정상화
다. 공분산도 단지 시차에만 의존, 실제 특정 시점 t, s에는 의존하지 않음
· 계절차분(seasonal difference) : 여러 시점 전의 자료를 뺴는 것 방법, 주로 계절성을 갖는 자료를 장상화 하는데 사용 |
라. 정상 시계열의 모습

4. 시계열모형
가. 자기 회귀 모형(AR 모형, autoregressive model)
· p 시점 전의 자료가 현재 자료에 영향을 주는 모형
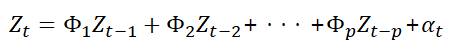


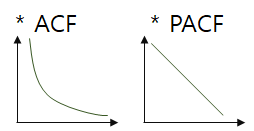
나. 이동평균 모형(MA 모형, Moving Average model)
· 유한한 개수의 백색잡음의 결합이므로 언제나 정상성을 만족
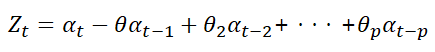
· AR 모형과 반대로 ACF에서 절단점을 갖고, PACF가 빠르게 감소
다. 자기회귀누적이동평균 모형(ARIMA(p,d,q) 모형, autoregressive integrated moving average model)
· ARIMA 모형은 비정상시계열 모형
· ARIMA 모형을 차분이나 변환을 통해 AR모형이나 MA모형, 이 둘을 합침 ARMA 모형으로 정상화 할 수 있음
· p는 AR 모형, q는 MA 모형과 관련이 있는 차수(ARIMA에서 ARMA로 정상화 할때 차분된 횟수 의미)
· d=0이면 ARMA(p,q) 모형
· p=0 이면 IMA(d,q) 모형이라고 부르고, d번 차분하면 MA(q) 모형
· q=-0 이면 ARI(p,d) 모형이라 부르며, d번 차분한 시계열이 AR(p) 모형
· p → AR, q → MA, d →ARMA
라. 분해시계열
· 시계열에 영향을 주는 일반적인 요인을 시계열에서 분리해 분석하는 방법
· 분해식의 일반적 정의
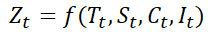

Start = 1871 End = 1970 Frequency = 1 [1] 1120 1160 963 1210 1160 1160 813 1230 1370 1140 995 935 1110 994 1020 960 1180 799 958 1140 [21] 1100 1210 1150 1250 1260 1220 1030 1100 774 840 874 694 940 833 701 916 692 1020 1050 969 [41] 831 726 456 824 702 1120 1100 832 764 821 768 845 864 862 698 845 744 796 1040 759 [61] 781 865 845 944 984 897 822 1010 771 676 649 846 812 742 801 1040 860 874 848 890 [81] 744 749 838 1050 918 986 797 923 975 815 1020 906 901 1170 912 746 919 718 714 740 > plot(Nile)
* plot(Nile)
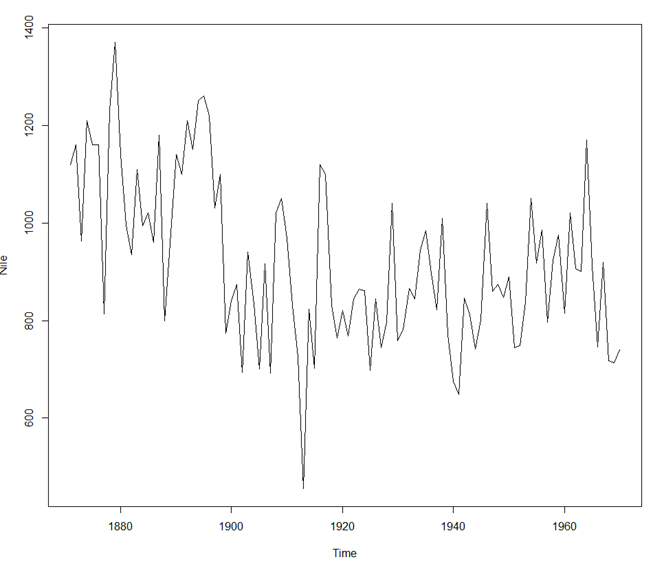
> #비정상 시계열 일정한 곡선유지해야 정상시계열 > #정상성 만족 못함 > #diff 함수 : 차분을 한다. > Nile.diff<-diff(Nile,differences = 1) > plot(Nile.diff)
* plot(Nile.diff)
> Nile.diff<-diff(Nile,differences = 1) > plot(Nile.diff)
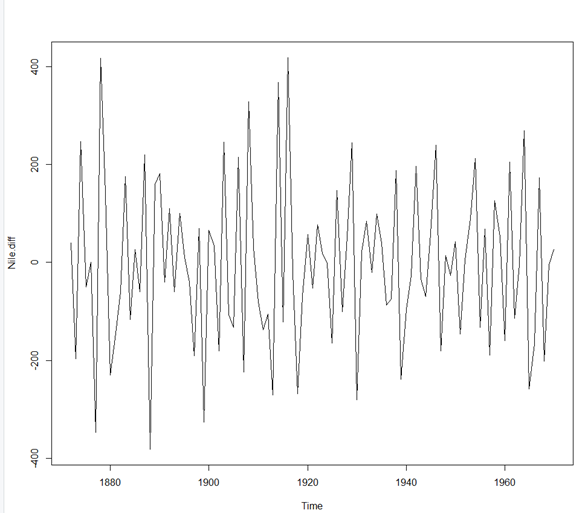
* plot(Nile.diff)
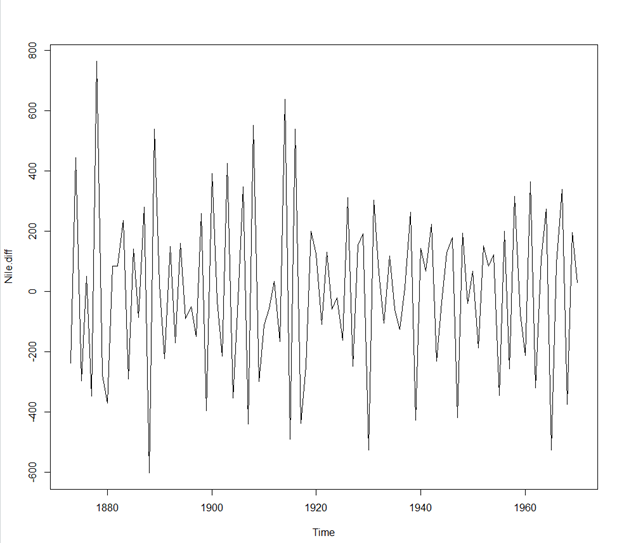
> ldeaths #폐질환 사망자에 관한 자료(1974~1979)
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1974 3035 2552 2704 2554 2014 1655 1721 1524 1596 2074 2199 2512
1975 2933 2889 2938 2497 1870 1726 1607 1545 1396 1787 2076 2837
1976 2787 3891 3179 2011 1636 1580 1489 1300 1356 1653 2013 2823
1977 3102 2294 2385 2444 1748 1554 1498 1361 1346 1564 1640 2293
1978 2815 3137 2679 1969 1870 1633 1529 1366 1357 1570 1535 2491
1979 3084 2605 2573 2143 1693 1504 1461 1354 1333 1492 1781 1915
> #겨울에 폐질환환자 증가(계절성요인영향을 받음)
> #계절성 빼고 확인
> plot(ldeaths)* plot(ldeaths)
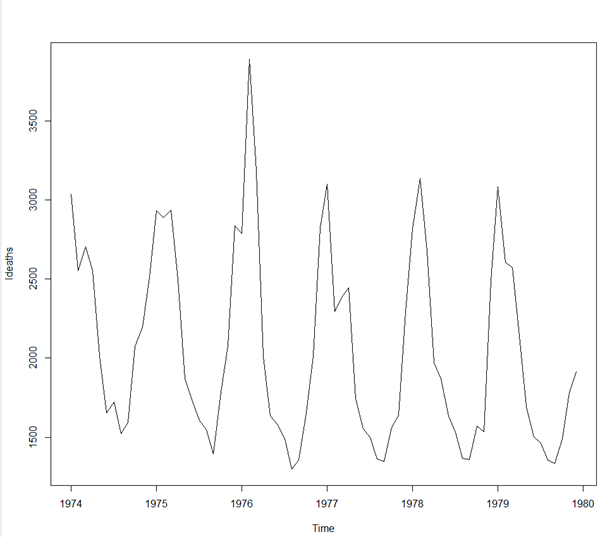
> # decompose()함수 : 시계열 자료를4가지 요인으로 분해
> ldeaths.decomp<-decompose(ldeaths)
> ldeaths.decomp$seasonal
Jan Feb Mar Apr May Jun Jul Aug Sep Oct
1974 873.7514 896.3347 687.5431 156.5847 -284.4819 -440.0236 -519.4236 -669.8736 -678.2236 -354.3069
1975 873.7514 896.3347 687.5431 156.5847 -284.4819 -440.0236 -519.4236 -669.8736 -678.2236 -354.3069
1976 873.7514 896.3347 687.5431 156.5847 -284.4819 -440.0236 -519.4236 -669.8736 -678.2236 -354.3069
1977 873.7514 896.3347 687.5431 156.5847 -284.4819 -440.0236 -519.4236 -669.8736 -678.2236 -354.3069
1978 873.7514 896.3347 687.5431 156.5847 -284.4819 -440.0236 -519.4236 -669.8736 -678.2236 -354.3069
1979 873.7514 896.3347 687.5431 156.5847 -284.4819 -440.0236 -519.4236 -669.8736 -678.2236 -354.3069
Nov Dec
1974 -185.2069 517.3264
1975 -185.2069 517.3264
1976 -185.2069 517.3264
1977 -185.2069 517.3264
1978 -185.2069 517.3264
1979 -185.2069 517.3264
> plot(ldeaths.decomp)* plot(ldeath.decomp)
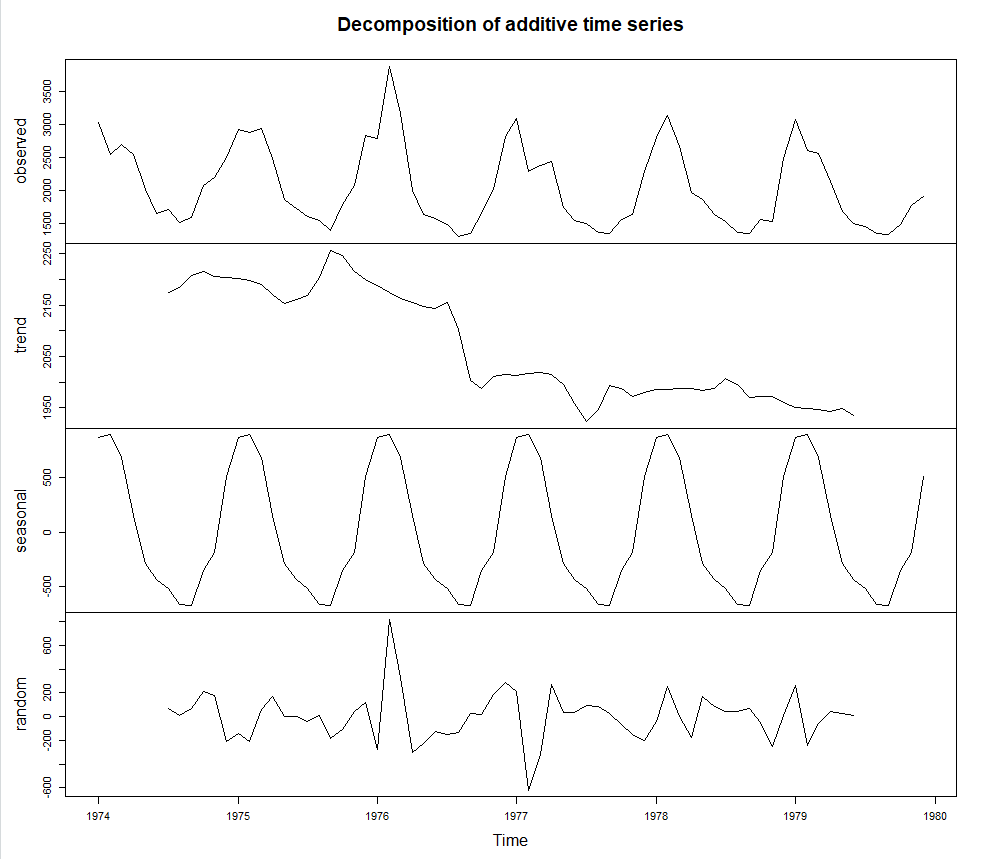
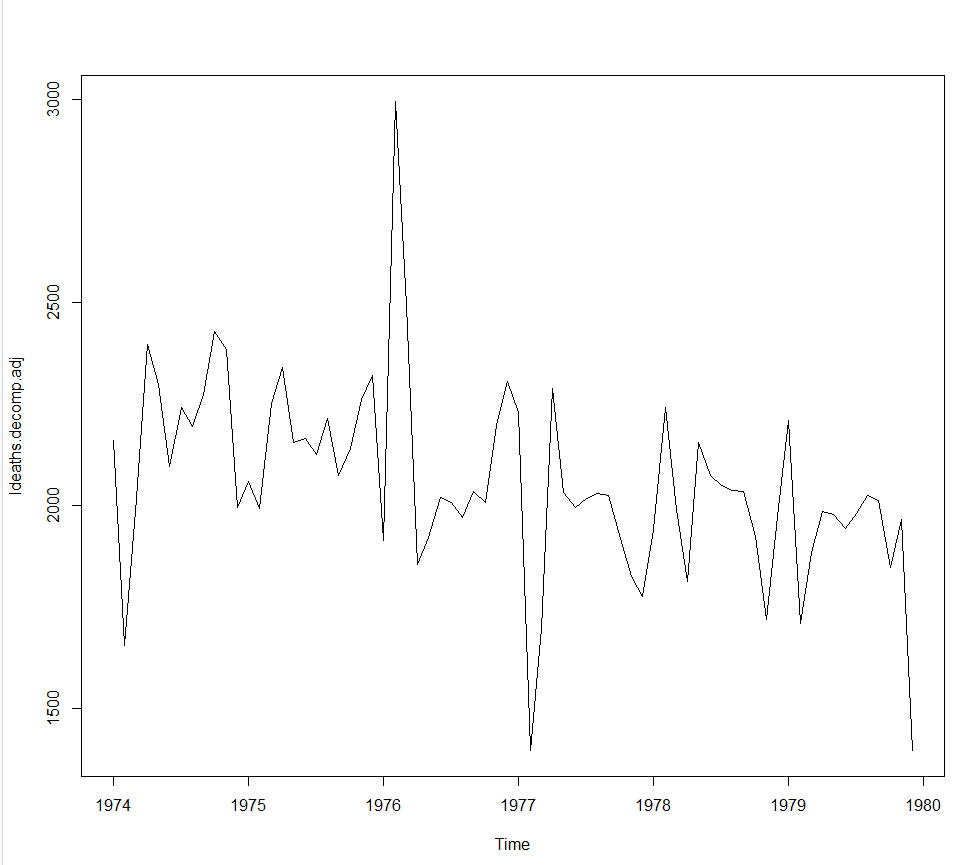
> ldeaths.decomp.adj<-ldeaths -ldeaths.decomp$seasonal > plot(ldeaths.decomp.adj)
* plot(ldeaths.decomp.adj)
6절 주성분 분석
1. 주성분분석(Principal Component Analysis)
· 고차원의 데이터(차원축소)를 저차원의 데이터로 환원시키는 기법
· 서로 상관성이 높은 변수들의 선형결합
· 고유벡터 기반의 대변량 분석들 중 가장 쉬움
· 데이터 분포를 가장 크게 설명하는 축을 중심으로 설명함
2. 주성분분석의 목적
· 상관성이 없는(적은) 주성분으로 변수들을 축소
· 군집분석을 수행하면 군집화 결과와 연산속도를 개선
3. 주성분분석 vs 요인분석
가. 요인분석(Factor Analysis)
· 등간척도(혹은 비율척도)로 측정한 두 개 이상의 변수들에 잠재되어 있는 공통인자를 찾아내는 기법
나. 공통점
· 데이터를 축소하는데 사용
· 원래 데이터를 활용해서 몇개의 새로운 변수들을 만들 수 있음.
다. 차이점
1)생성된 변수의수
· 요인분석은 몇 개라고 지정 없이 만들수 있음.
· 주성분분석은 제1주성분, 제2주성분, 제3주성분 정도로 활용
2)생성된 변수 이름
· 요인분석은 분석자가 요인의 이름을 명명
· 주성분분석은 주로 제1주성분, 제2주성분 등으로 표현
3) 생성된 변수들 간의 관계
· 요인분석은 새 변수들은 기본적으로 대등한 관계를 갖고 '어떤 것이 더 중요하다'라는 의미는 요인분석에서는 없음.
· 주성분분석은 제1주성분이 가장 중요하고, 그 다음 제2주성분이 중요하게 취급
4)분석방법의 의미
· 요인분석은 목표변수를 고려하지 않고 그냥 데이터가 주어지면 변수들은 비슷한 성격들로 묶어서 새로운 [잠재]변수들은 만듬.
· 주성분분석은 목표 변수를 고려하여 목표 변수를 잘 예측/분류하기 위하여 원래 변수들의 선형 결합으로 이루어진 몇개의 주성분(변수)들을 찾아냄.
4. 주성분의 선택법
· 주성분분석의 결과에서 누적기여율(cumulative proportion)이 85%이상이면 주성분의 수로 결정
· scree plot을 활용하여 고유값(eigenvalue)이 수명을 유지하기 전단계로 주성분의 수를 선택
'ADSP' 카테고리의 다른 글
| PART 03 데이터 분석 - 3 (0) | 2020.03.14 |
|---|---|
| PART 03 데이터 분석 - 1 (0) | 2020.02.24 |
| PART 02. 데이터 분석 기획 (0) | 2020.02.23 |
| PART 01. 데이터 이해 (0) | 2020.02.22 |
| [ADSP] R Studio설치 (0) | 2020.01.21 |



